Analyse de l’actionneur électromagnétique linéaire à l’aide de la FEA
RÉSUMÉ
Dans cet article, nous avons analysé les caractéristiques dynamiques d’un actionneur électromagnétique, utilisé pour les disjoncteurs à vide. Les phénomènes magnétiques, électriques et mécaniques sont analysés simultanément pour obtenir le comportement dynamique de l’actionneur. Les paramètres magnétiques sont calculés à l’aide de l’analyse par éléments finis (FEA), puis importés dans un logiciel d’analyse dynamique, où les équations électriques et mécaniques sont calculées. Les résultats de l’analyse ainsi que certaines données expérimentales sont présentés. Cette technique peut être utilisée pour analyser de manière très précise le comportement électromagnétique dynamique des capteurs, relais, commutateurs et autres systèmes d’actionneurs.
ÉNONCÉ DU PROBLÈME
L’actionneur électromagnétique est largement utilisé dans les disjoncteurs. Son rôle consiste à mettre en mouvement les contacts mobiles de la bouteille sous vide selon certaines vitesses et trajectoires précises.
Dans ce rapport, un nouveau modèle d’actionneur linéaire, qui sera utilisé dans la nouvelle génération des systèmes TE de ligne de toit de matériel roulant, est proposé et analysé. Un facteur qui affecte de manière significative le fonctionnement de l’actionneur est la force de traînée magnétique. Cette force pourrait être due à :
- Champ magnétique statique : lorsque l’armature se déplace, elle subit une traction magnétique (due au mouvement relatif avec les aimants en fonction de leur position).
- Courant résiduel de la bobine : lorsque la tension de maintien est déconnectée de la bobine, il faut du temps pour que le courant de la bobine chute à zéro. Lorsqu’il est présent, il produit une traction magnétique vers la position de fermeture. La diminution rapide du courant peut être obtenue par :
o Augmentation de la tension TVS (suppresseur de surtension)
o Diminution de l’inductance de la bobine
- Courants de Foucault induits [1]
- Courants de Foucault induits par le mouvement : cet effet représente la majorité des pertes d’énergie (s’il y a un mouvement relatif entre l’armature et les aimants). Il peut être efficacement réduit, voire éliminé, en déplaçant les aimants dans l’armature (et/ou en utilisant des aimants à intensité de champ magnétique réduite) [1].
- Courant EMF (Force électromotrice) arrière : l’armature en mouvement provoque une tension EMF arrière, qui entraîne à son tour un courant EMF arrière qui agit contre le mouvement.
Les recherches antérieures ne tiennent pas compte de l’effet des courants de Foucault dans le mouvement de l’armature de l’actionneur mais, comme elles sont essentielles pour la performance de l’actionneur, tous les effets mentionnés ci-dessus ont été pris en considération, calculés et inclus dans le modèle. Ainsi, notre modèle prédit avec une grande précision le comportement réel de l’actionneur avant le prototypage et peut être utilisé pour l’analyse de sensibilité afin de réduire le temps de conception et les coûts, et de proposer une solution technique et économique optimale. Une description plus détaillée des méthodes et des résultats suivra dans les sections suivantes.
MÉTHODES ET RÉSULTATS
Analyse statique
La figure 1 illustre la structure proposée de l’actionneur électromagnétique :
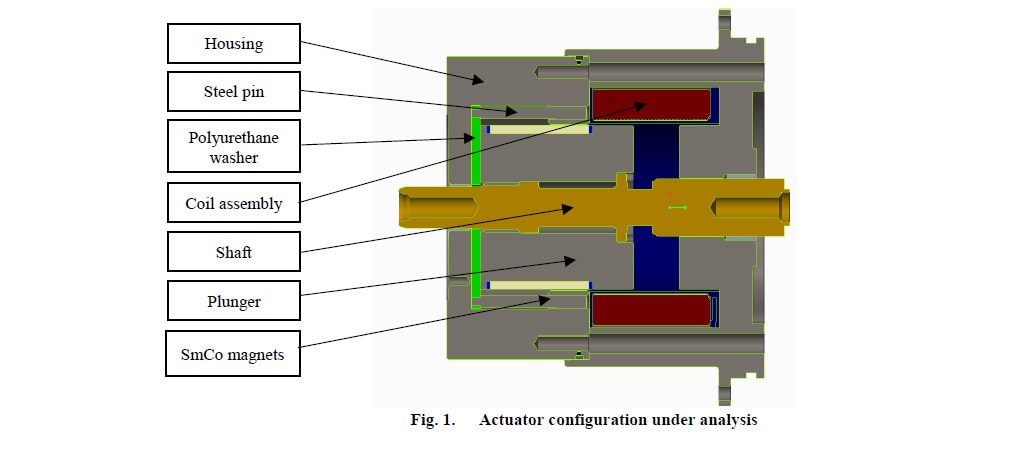
Par rapport à un actionneur type (qui se compose généralement d’une bobine d’ouverture et d’une bobine de fermeture), ce type d’actionneur se compose du boîtier (ou cadre), de la broche en acier, de l’ensemble bobine (bobine et enroulement), de l’armature (piston), de l’arbre, de la rondelle en polyuréthane et des aimants permanents SmCo (Samarium Cobalt) (PM).
Les enroulements de bobine créent un champ électromagnétique lorsque le courant est appliqué sur ses bornes. Le but de la bobine est d’entraîner l’armature en position fermée et de l’aider à la maintenir à cet endroit. Cet actionneur doit disposer d’un mécanisme de sécurité intégrée (ouvert) en cas de perte de puissance dans la bobine. Le processus d’ouverture commence lorsque le courant dans la bobine est coupé et n’est obtenu qu’à l’aide
de moyens mécaniques (ressorts, etc.). Ainsi, la puissance dissipée (critique pour les trains modernes) dans ce type d’actionneur est nettement inférieure à la dissipation dans un actionneur type, tandis que la sécurité est prioritaire.
Le stator concentre le champ magnétique. Il entoure l’extérieur de la bobine et est fabriqué en acier à faible teneur en carbone AISI (American Iron and Steel Institute) 1018. L’acier à faible teneur en carbone est utilisé pour la plupart des actionneurs électromagnétiques. Il a une perméabilité élevée et un coût relativement faible [12].
Les aimants produisent une force de maintien, qui dépend de la position de l’armature par rapport au boîtier (réluctance magnétique faible et élevée).
Pour l’analyse, la physique des champs magnétiques a été sélectionnée. Pour définir les propriétés magnétiques non linéaires de l’acier au carbone et la densité de flux rémanente des aimants, la loi d’Ampère a été appliquée aux domaines pertinents. Les propriétés magnétiques non linéaires sont introduites pour tenir compte de la saturation magnétique (l’état où l’aimantation d’un
matériau atteint un point où il ne peut plus augmenter en raison de l’augmentation du champ magnétique externe appliqué H) [2] [3].
Pour le calcul de la force électromagnétique dans l’armature, la méthode du tenseur de contrainte de Maxwell a été appliquée. Ce tenseur est mathématiquement une intégrale le long d’un chemin fermé (en 2D) ou d’une surface fermée « A » (en 3D) autour d’un domaine d’intérêt. L’une des limites de cette méthode est que, lorsqu’il existe une interface matériau magnétique-matériau magnétique (agissant comme des pôles), un très petit espace d’air (< 0,1 mm) doit être maintenu entre eux, sinon une valeur très faible de la force est calculée, qui ne correspond pas à sa valeur réelle [12] [5].
Analyse dynamique
Pour étudier le comportement dynamique de l’actionneur, deux modèles ont été simulés pour tenir compte de ses performances d’ouverture et de fermeture [4] [7] [8]. Le circuit électrique utilisé pour entraîner l’actionneur est illustré ci-dessous (figure 2) :
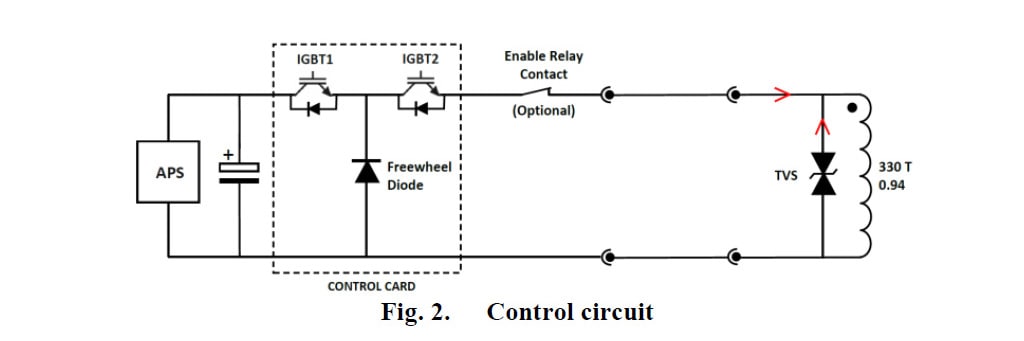
Lors de l’ouverture, le courant dans la bobine est coupé et le TVS est utilisé pour supprimer la tension induite (et par conséquent le courant induit). Lors de la fermeture, une séquence d’impulsions de l’APS (source d’alimentation de l’actionneur) est utilisée pour entraîner l’actionneur.
Les équations résolues ((1) – (3)) sont les suivantes :
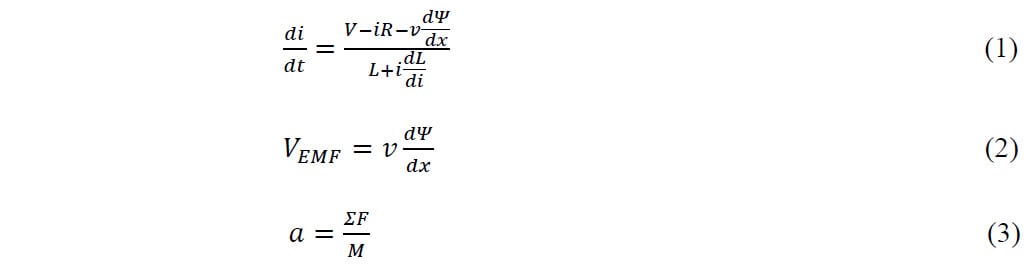
V : tension (V), i : courant (A), R : résistance (Ω), L : inductance (H), VEMF : tension EMF arrière (V), v : vitesse (m/s), α : accélération (m/s2), t : temps (s), ΣF : force totale (N), M : masse (kg), Ψ : liaison de flux (Wb-T). Les liaisons de flux ont deux composantes, l’une dépendant du champ magnétique produit par le PM (BPM) et l’autre du champ magnétique produit par la bobine (Bc).
Les courants de Foucault ont été calculés à l’aide de l’équation suivante [1] :
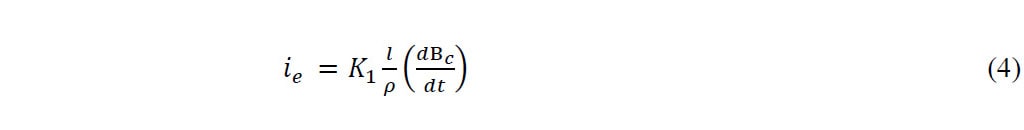
Où K1 est un facteur géométrique, l est la longueur du piston et ρ est la résistivité du matériau [1]. En supposant que le piston est un cylindre, l’équation 4 devient :

Le champ magnétique produit par les courants de Foucault (Be) et la force correspondante (Fe) ont été calculés à l’aide des équations 6 et 7.
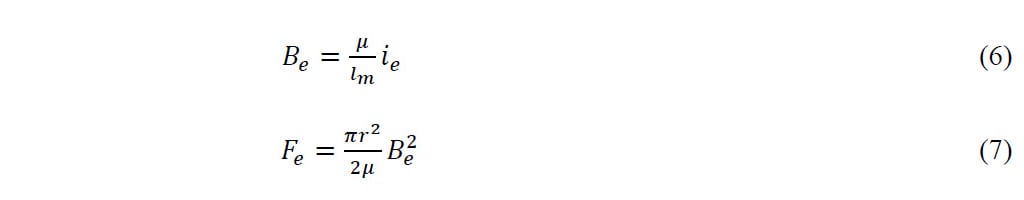
Où lm est le chemin magnétique, r est le rayon du piston et μ la permittivité du matériau.
Résultats de la simulation
La distribution du champ magnétique à différentes positions est illustrée à la figure 3.
En position fermée (figure 3a), l’armature avec le boîtier en acier forme un chemin de faible réluctance magnétique, tandis que le grand espace au sommet représente un chemin de résistance magnétique élevée. Par conséquent, les lignes de champ magnétique traversent presque exclusivement l’extrémité de l’armature en contact avec le boîtier. La force de maintien produite par les aimants dans cette
position est de grande valeur. Pour obtenir un fonctionnement à sécurité intégrée, la bobine est également utilisée afin de produire une force de maintien encore plus élevée pour maintenir l’armature en position fermée.
Pour l’ouvrir, le courant circulant à travers la bobine est coupé et l’armature commence à bouger. À mesure que l’armature passe d’une position fermée à une position ouverte, les lignes de champ magnétique sont poussées vers le chemin précédemment plus bas (figure 3b) car maintenant, l’espace d’air en position ouverte est de plus en plus étroit (la réticence magnétique diminue). Par conséquent, la force de maintien en bas diminue, tandis que l’attraction en haut augmente.
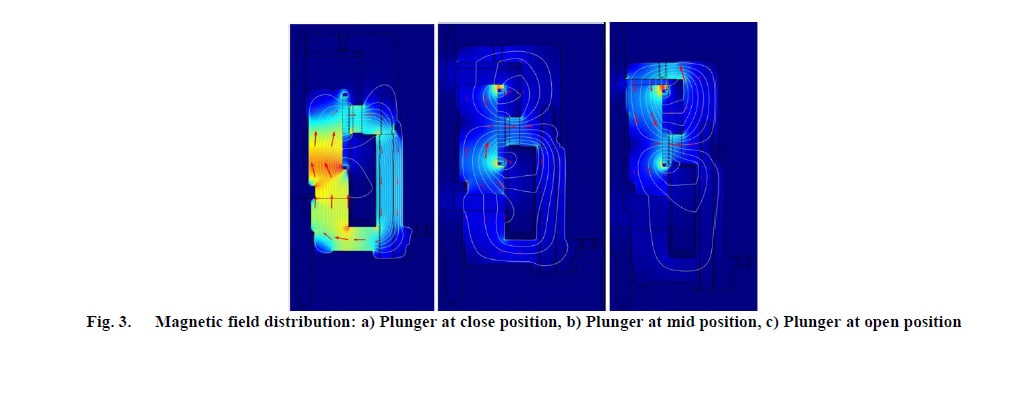
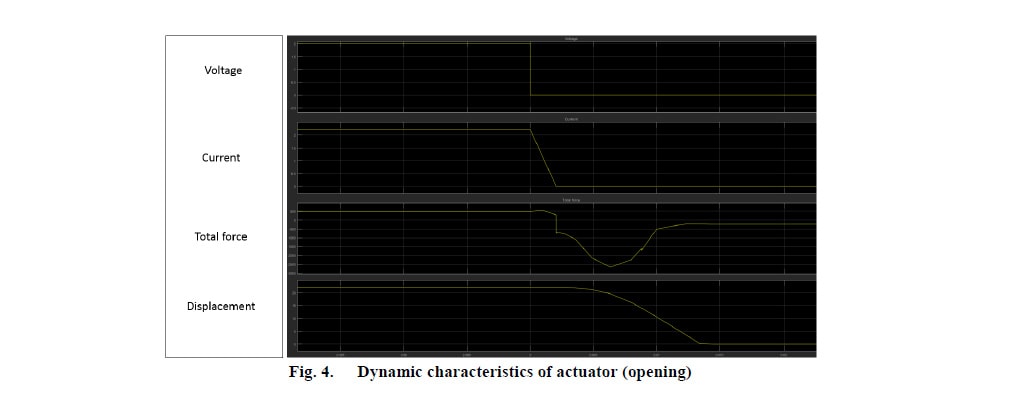
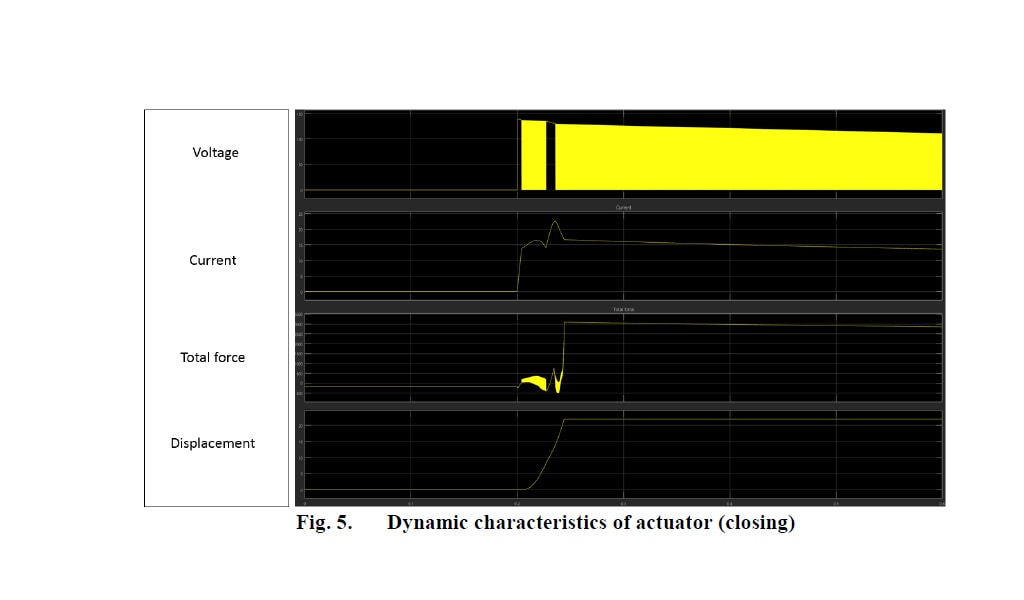
Lorsque l’armature atteint la position ouverte (figure 3c), le chemin de réluctance est opposé à celui mentionné précédemment, de sorte que les lignes de champ magnétique sont principalement concentrées au sommet. Comme indiqué, la concentration du champ magnétique n’est pas similaire lorsque l’armature est en position fermée et ouverte. Par conséquent, la force de maintien à la position ouverte aura une valeur inférieure à celle en position fermée. Les résultats de l’analyse dynamique sont présentés dans les figures 4 et 5 :
Quelques résultats expérimentaux préliminaires (figures 6 et 7) dans des modèles d’actionneurs légèrement différents (conceptions avant les ajustements finaux) démontrent le concept du modèle et du circuit de commande proposés.
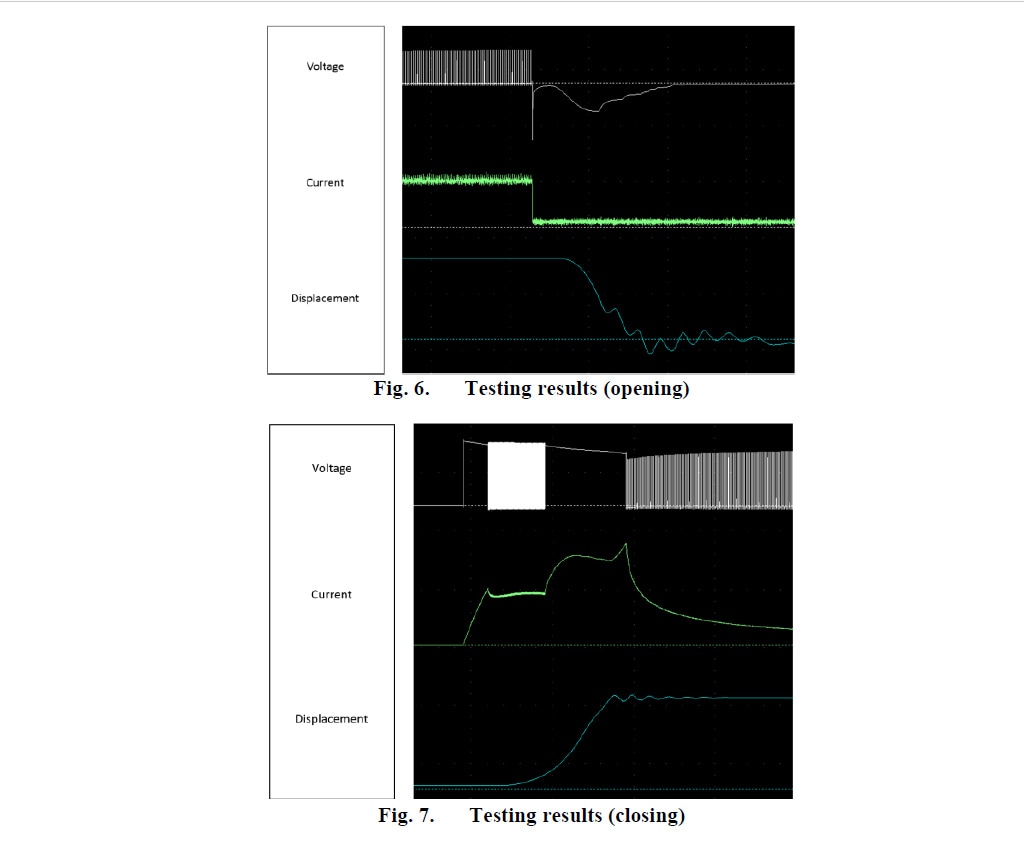
Le profil des caractéristiques dynamiques observées lors des essais est conforme aux résultats de la simulation. Les valeurs de vitesse et de durée de l’opération de fermeture et d’ouverture sont similaires dans les tests et les simulations (moins de 10 % d’erreur).
DISCUSSION ET POINTS CLÉS
Le modèle optimisé de l’actionneur est proposé pour minimiser, voire éliminer, l’effet du freinage électromagnétique dû à l’induction. Un nouveau circuit de commande est utilisé pour supprimer cet effet lors de l’ouverture, tandis que, lors de la fermeture, une séquence de pulsation est introduite pour contrôler les performances de l’actionneur.
La conception innovante de l’actionneur et le circuit de commande qui améliore le rendement et les performances du système (faible puissance dissipée) contribuent de manière significative au développement continu de la nouvelle génération de systèmes de ligne de toit de train TE. L’actionneur est conçu pour offrir un fonctionnement fiable et satisfait aux exigences de profil bas et léger du marché
(amélioration des performances aérodynamiques) et de consommation d’énergie minimale.
La comparaison entre les résultats des essais et des simulations permet de conclure que la méthode de calcul proposée est capable d’analyser avec précision les caractéristiques transitoires d’un actionneur électromagnétique. Il convient également de mentionner que la contribution des courants de Foucault est prise en compte dans le présent rapport, ce qui n’est pas le cas dans la plupart des articles existants en raison de la
complexité de sa formulation. Par conséquent, l’importance de cette méthode est qu’elle peut être utilisée avant le prototypage pour réduire considérablement le temps, les coûts et les ressources lors de la conception et de la fabrication.
REMERCIEMENTS
Nous tenons à remercier Graham Mcdonald, Robert Phillpotts et Thomas Moore pour leur soutien et leurs conseils d’experts tout au long de ce projet. Ils ont fourni les modèles mécaniques et les configurations électroniques en suivant les recommandations de l’analyse et les données pour les forces mécaniques.
RÉFÉRENCES
[1] Mandache, L. ; D. Topan ; K. Al Haddad. « Modélisation des noyaux ferromagnétiques non linéaires ». Revue Roumaine de Sciences Techniques. Série Électrotechnique et Énergétique. Vol. 53, Numéro 4. 2008.
[2] K. Srairi et M. Feliachi, « Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators », IEEE Transactions on Magnetics, vol. 34, numéro 5, pages 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov et D. Dimitrov, « Dynamic characteristics of a permanent magnet electromagnetic valve actuator », lors de la 12e Conférence Internationale sur l’Optimisation des Équipements Électriques et Électroniques, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov et K. Hinov, « Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator », Elec. Energ., vol. 23, numéro 1, pages 37-43, 2010.
[5] I. Yatchev et E. Ritchie, « Simulation of Dynamics of a Permanent Manget Linear Actuator », Internation Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, numéro 6, pages 726-730, 2010.
[6] S.-M. Wang, T. Miyano et M. Hubbard, « Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator » IEEE Transactions on Magnetics, vol. 29, numéro 2, pages 1741-1746, 1993.
[7] A. Radulian et N. Mocioi, « Modélisation numérique d’un actionneur électromagnétique pour contacteurs à vide ». Conférence internationale et exposition sur le génie électrique et énergétique, Iasi, Roumanie, 2014.
[8] N. Paudel, « Part 1 : How to Model a Linear Electromagnetic Plunger », 7 juin 2016. [En ligne]. Disponible : https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, « Part 2: Model a Linear Electromagnetic Plunger with a Blocker », 14 juin 2016. [En ligne]. Disponible : https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer et B. Ulrych, « Electromechanical Actuators Dynamics » J. of Electrical Engineering, vol. 60, numéro 5, pages 255, 2009.
[11] H. Musaab, « Using Lookup Tables to Model an Electromagnetic Suspansion System », American Journal of Applied Sciences, vol. 9, numéro 8, pages 1199-1202, 2012.
[12] O. Vogel et J. Ulm, « Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics », lors de la Comsol Conference, Stuttgart, 2011.
Analyse de l’actionneur électromagnétique linéaire à l’aide de la FEA
RÉSUMÉ
Dans cet article, nous avons analysé les caractéristiques dynamiques d’un actionneur électromagnétique, utilisé pour les disjoncteurs à vide. Les phénomènes magnétiques, électriques et mécaniques sont analysés simultanément pour obtenir le comportement dynamique de l’actionneur. Les paramètres magnétiques sont calculés à l’aide de l’analyse par éléments finis (FEA), puis importés dans un logiciel d’analyse dynamique, où les équations électriques et mécaniques sont calculées. Les résultats de l’analyse ainsi que certaines données expérimentales sont présentés. Cette technique peut être utilisée pour analyser de manière très précise le comportement électromagnétique dynamique des capteurs, relais, commutateurs et autres systèmes d’actionneurs.
ÉNONCÉ DU PROBLÈME
L’actionneur électromagnétique est largement utilisé dans les disjoncteurs. Son rôle consiste à mettre en mouvement les contacts mobiles de la bouteille sous vide selon certaines vitesses et trajectoires précises.
Dans ce rapport, un nouveau modèle d’actionneur linéaire, qui sera utilisé dans la nouvelle génération des systèmes TE de ligne de toit de matériel roulant, est proposé et analysé. Un facteur qui affecte de manière significative le fonctionnement de l’actionneur est la force de traînée magnétique. Cette force pourrait être due à :
- Champ magnétique statique : lorsque l’armature se déplace, elle subit une traction magnétique (due au mouvement relatif avec les aimants en fonction de leur position).
- Courant résiduel de la bobine : lorsque la tension de maintien est déconnectée de la bobine, il faut du temps pour que le courant de la bobine chute à zéro. Lorsqu’il est présent, il produit une traction magnétique vers la position de fermeture. La diminution rapide du courant peut être obtenue par :
o Augmentation de la tension TVS (suppresseur de surtension)
o Diminution de l’inductance de la bobine
- Courants de Foucault induits [1]
- Courants de Foucault induits par le mouvement : cet effet représente la majorité des pertes d’énergie (s’il y a un mouvement relatif entre l’armature et les aimants). Il peut être efficacement réduit, voire éliminé, en déplaçant les aimants dans l’armature (et/ou en utilisant des aimants à intensité de champ magnétique réduite) [1].
- Courant EMF (Force électromotrice) arrière : l’armature en mouvement provoque une tension EMF arrière, qui entraîne à son tour un courant EMF arrière qui agit contre le mouvement.
Les recherches antérieures ne tiennent pas compte de l’effet des courants de Foucault dans le mouvement de l’armature de l’actionneur mais, comme elles sont essentielles pour la performance de l’actionneur, tous les effets mentionnés ci-dessus ont été pris en considération, calculés et inclus dans le modèle. Ainsi, notre modèle prédit avec une grande précision le comportement réel de l’actionneur avant le prototypage et peut être utilisé pour l’analyse de sensibilité afin de réduire le temps de conception et les coûts, et de proposer une solution technique et économique optimale. Une description plus détaillée des méthodes et des résultats suivra dans les sections suivantes.
MÉTHODES ET RÉSULTATS
Analyse statique
La figure 1 illustre la structure proposée de l’actionneur électromagnétique :

Par rapport à un actionneur type (qui se compose généralement d’une bobine d’ouverture et d’une bobine de fermeture), ce type d’actionneur se compose du boîtier (ou cadre), de la broche en acier, de l’ensemble bobine (bobine et enroulement), de l’armature (piston), de l’arbre, de la rondelle en polyuréthane et des aimants permanents SmCo (Samarium Cobalt) (PM).
Les enroulements de bobine créent un champ électromagnétique lorsque le courant est appliqué sur ses bornes. Le but de la bobine est d’entraîner l’armature en position fermée et de l’aider à la maintenir à cet endroit. Cet actionneur doit disposer d’un mécanisme de sécurité intégrée (ouvert) en cas de perte de puissance dans la bobine. Le processus d’ouverture commence lorsque le courant dans la bobine est coupé et n’est obtenu qu’à l’aide
de moyens mécaniques (ressorts, etc.). Ainsi, la puissance dissipée (critique pour les trains modernes) dans ce type d’actionneur est nettement inférieure à la dissipation dans un actionneur type, tandis que la sécurité est prioritaire.
Le stator concentre le champ magnétique. Il entoure l’extérieur de la bobine et est fabriqué en acier à faible teneur en carbone AISI (American Iron and Steel Institute) 1018. L’acier à faible teneur en carbone est utilisé pour la plupart des actionneurs électromagnétiques. Il a une perméabilité élevée et un coût relativement faible [12].
Les aimants produisent une force de maintien, qui dépend de la position de l’armature par rapport au boîtier (réluctance magnétique faible et élevée).
Pour l’analyse, la physique des champs magnétiques a été sélectionnée. Pour définir les propriétés magnétiques non linéaires de l’acier au carbone et la densité de flux rémanente des aimants, la loi d’Ampère a été appliquée aux domaines pertinents. Les propriétés magnétiques non linéaires sont introduites pour tenir compte de la saturation magnétique (l’état où l’aimantation d’un
matériau atteint un point où il ne peut plus augmenter en raison de l’augmentation du champ magnétique externe appliqué H) [2] [3].
Pour le calcul de la force électromagnétique dans l’armature, la méthode du tenseur de contrainte de Maxwell a été appliquée. Ce tenseur est mathématiquement une intégrale le long d’un chemin fermé (en 2D) ou d’une surface fermée « A » (en 3D) autour d’un domaine d’intérêt. L’une des limites de cette méthode est que, lorsqu’il existe une interface matériau magnétique-matériau magnétique (agissant comme des pôles), un très petit espace d’air (< 0,1 mm) doit être maintenu entre eux, sinon une valeur très faible de la force est calculée, qui ne correspond pas à sa valeur réelle [12] [5].
Analyse dynamique
Pour étudier le comportement dynamique de l’actionneur, deux modèles ont été simulés pour tenir compte de ses performances d’ouverture et de fermeture [4] [7] [8]. Le circuit électrique utilisé pour entraîner l’actionneur est illustré ci-dessous (figure 2) :

Lors de l’ouverture, le courant dans la bobine est coupé et le TVS est utilisé pour supprimer la tension induite (et par conséquent le courant induit). Lors de la fermeture, une séquence d’impulsions de l’APS (source d’alimentation de l’actionneur) est utilisée pour entraîner l’actionneur.
Les équations résolues ((1) – (3)) sont les suivantes :
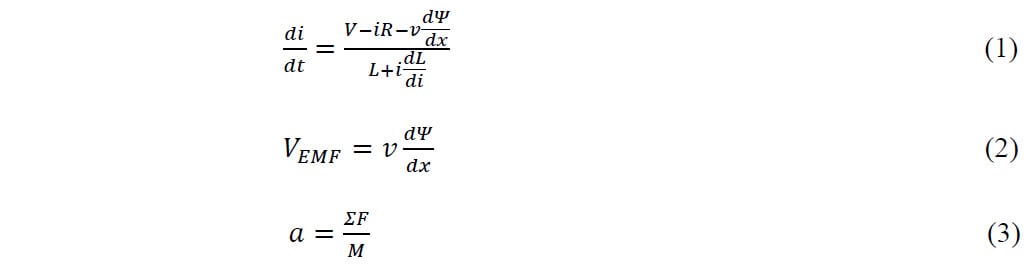
V : tension (V), i : courant (A), R : résistance (Ω), L : inductance (H), VEMF : tension EMF arrière (V), v : vitesse (m/s), α : accélération (m/s2), t : temps (s), ΣF : force totale (N), M : masse (kg), Ψ : liaison de flux (Wb-T). Les liaisons de flux ont deux composantes, l’une dépendant du champ magnétique produit par le PM (BPM) et l’autre du champ magnétique produit par la bobine (Bc).
Les courants de Foucault ont été calculés à l’aide de l’équation suivante [1] :
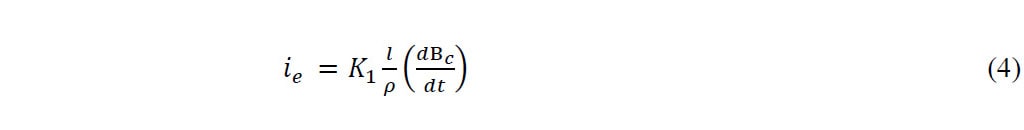
Où K1 est un facteur géométrique, l est la longueur du piston et ρ est la résistivité du matériau [1]. En supposant que le piston est un cylindre, l’équation 4 devient :

Le champ magnétique produit par les courants de Foucault (Be) et la force correspondante (Fe) ont été calculés à l’aide des équations 6 et 7.
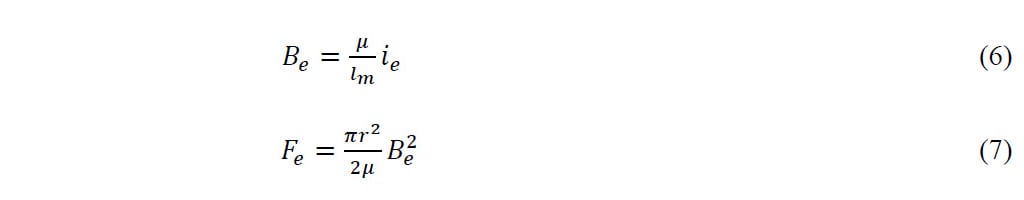
Où lm est le chemin magnétique, r est le rayon du piston et μ la permittivité du matériau.
Résultats de la simulation
La distribution du champ magnétique à différentes positions est illustrée à la figure 3.
En position fermée (figure 3a), l’armature avec le boîtier en acier forme un chemin de faible réluctance magnétique, tandis que le grand espace au sommet représente un chemin de résistance magnétique élevée. Par conséquent, les lignes de champ magnétique traversent presque exclusivement l’extrémité de l’armature en contact avec le boîtier. La force de maintien produite par les aimants dans cette
position est de grande valeur. Pour obtenir un fonctionnement à sécurité intégrée, la bobine est également utilisée afin de produire une force de maintien encore plus élevée pour maintenir l’armature en position fermée.
Pour l’ouvrir, le courant circulant à travers la bobine est coupé et l’armature commence à bouger. À mesure que l’armature passe d’une position fermée à une position ouverte, les lignes de champ magnétique sont poussées vers le chemin précédemment plus bas (figure 3b) car maintenant, l’espace d’air en position ouverte est de plus en plus étroit (la réticence magnétique diminue). Par conséquent, la force de maintien en bas diminue, tandis que l’attraction en haut augmente.

Lorsque l’armature atteint la position ouverte (figure 3c), le chemin de réluctance est opposé à celui mentionné précédemment, de sorte que les lignes de champ magnétique sont principalement concentrées au sommet. Comme indiqué, la concentration du champ magnétique n’est pas similaire lorsque l’armature est en position fermée et ouverte. Par conséquent, la force de maintien à la position ouverte aura une valeur inférieure à celle en position fermée. Les résultats de l’analyse dynamique sont présentés dans les figures 4 et 5 :


Quelques résultats expérimentaux préliminaires (figures 6 et 7) dans des modèles d’actionneurs légèrement différents (conceptions avant les ajustements finaux) démontrent le concept du modèle et du circuit de commande proposés.

Le profil des caractéristiques dynamiques observées lors des essais est conforme aux résultats de la simulation. Les valeurs de vitesse et de durée de l’opération de fermeture et d’ouverture sont similaires dans les tests et les simulations (moins de 10 % d’erreur).
DISCUSSION ET POINTS CLÉS
Le modèle optimisé de l’actionneur est proposé pour minimiser, voire éliminer, l’effet du freinage électromagnétique dû à l’induction. Un nouveau circuit de commande est utilisé pour supprimer cet effet lors de l’ouverture, tandis que, lors de la fermeture, une séquence de pulsation est introduite pour contrôler les performances de l’actionneur.
La conception innovante de l’actionneur et le circuit de commande qui améliore le rendement et les performances du système (faible puissance dissipée) contribuent de manière significative au développement continu de la nouvelle génération de systèmes de ligne de toit de train TE. L’actionneur est conçu pour offrir un fonctionnement fiable et satisfait aux exigences de profil bas et léger du marché
(amélioration des performances aérodynamiques) et de consommation d’énergie minimale.
La comparaison entre les résultats des essais et des simulations permet de conclure que la méthode de calcul proposée est capable d’analyser avec précision les caractéristiques transitoires d’un actionneur électromagnétique. Il convient également de mentionner que la contribution des courants de Foucault est prise en compte dans le présent rapport, ce qui n’est pas le cas dans la plupart des articles existants en raison de la
complexité de sa formulation. Par conséquent, l’importance de cette méthode est qu’elle peut être utilisée avant le prototypage pour réduire considérablement le temps, les coûts et les ressources lors de la conception et de la fabrication.
REMERCIEMENTS
Nous tenons à remercier Graham Mcdonald, Robert Phillpotts et Thomas Moore pour leur soutien et leurs conseils d’experts tout au long de ce projet. Ils ont fourni les modèles mécaniques et les configurations électroniques en suivant les recommandations de l’analyse et les données pour les forces mécaniques.
RÉFÉRENCES
[1] Mandache, L. ; D. Topan ; K. Al Haddad. « Modélisation des noyaux ferromagnétiques non linéaires ». Revue Roumaine de Sciences Techniques. Série Électrotechnique et Énergétique. Vol. 53, Numéro 4. 2008.
[2] K. Srairi et M. Feliachi, « Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators », IEEE Transactions on Magnetics, vol. 34, numéro 5, pages 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov et D. Dimitrov, « Dynamic characteristics of a permanent magnet electromagnetic valve actuator », lors de la 12e Conférence Internationale sur l’Optimisation des Équipements Électriques et Électroniques, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov et K. Hinov, « Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator », Elec. Energ., vol. 23, numéro 1, pages 37-43, 2010.
[5] I. Yatchev et E. Ritchie, « Simulation of Dynamics of a Permanent Manget Linear Actuator », Internation Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, numéro 6, pages 726-730, 2010.
[6] S.-M. Wang, T. Miyano et M. Hubbard, « Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator » IEEE Transactions on Magnetics, vol. 29, numéro 2, pages 1741-1746, 1993.
[7] A. Radulian et N. Mocioi, « Modélisation numérique d’un actionneur électromagnétique pour contacteurs à vide ». Conférence internationale et exposition sur le génie électrique et énergétique, Iasi, Roumanie, 2014.
[8] N. Paudel, « Part 1 : How to Model a Linear Electromagnetic Plunger », 7 juin 2016. [En ligne]. Disponible : https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, « Part 2: Model a Linear Electromagnetic Plunger with a Blocker », 14 juin 2016. [En ligne]. Disponible : https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer et B. Ulrych, « Electromechanical Actuators Dynamics » J. of Electrical Engineering, vol. 60, numéro 5, pages 255, 2009.
[11] H. Musaab, « Using Lookup Tables to Model an Electromagnetic Suspansion System », American Journal of Applied Sciences, vol. 9, numéro 8, pages 1199-1202, 2012.
[12] O. Vogel et J. Ulm, « Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics », lors de la Comsol Conference, Stuttgart, 2011.
