FEA による線形電磁アクチュエータの解析
要約
本ホワイトペーパーでは、真空遮断器に使用する電磁アクチュエータの動的特性を解析します。磁気的現象、電気的現象、機械的現象を同時に解析して、アクチュエータの動的な動作を把握します。有限要素解析 (FEA) を使用して磁気パラメータを計算し、その結果を動的解析ソフトウェアにインポートして電気的方程式と機械的方程式を計算します。その解析結果をいくつかの実験データとともに提示します。この技法は、センサ、リレー、スイッチなど他のアクチュエータ システムの動的な電磁動作をきわめて正確に解析する際に使用できます。
問題の提示
電磁アクチュエータは回路ブレーカで広く使用されています。その役割は、真空ボトル中の可動接点が特定の速度と正確な軌道で動作できるようにすることにあります。
このレポートでは、TE の新世代鉄道車両屋根上システムに使用する線形アクチュエータの新たなモデルを提案し、解析します。このアクチュエータの動作に著しく影響する要因はマグネットの抗力です。この力は次の原因で発生します。
- 静的磁界: アーマチュアが動作するときは、それに磁気的吸引力が働いています。この吸引力は、マグネットの位置に応じて、マグネットとアーマチュアとの間で発生する相対的運動に起因しています。
- コイル残留電流: コイルへの保持電圧供給を停止しても、コイル電流がゼロに低下するにはわずかな時間を要します。電流が残留している間は、閉路位置へ接点を引っ張る磁力が生成されます。この電流を迅速に抑制するには次の手段があります。
o TVS (過渡電圧抑制) 電圧を高くする
o コイルのインダクタンスを少なくする
- 誘導される渦電流 [1]
- 運動によって誘導される渦電流: エネルギ損失のほとんどはこの効果が占めており (アーマチュアとマグネットの間で相対的な運動が発生する場合)、アーマチュアの中をマグネットが移動する構造にすること (あるいは、磁界強度が低いマグネットを使用すること、またはこの両方の方法をとること) により、効果的に低減または排除できます。[1]
- 逆起電力 (起電力) による電流: アーマチュアが移動すると逆起電力による電圧が発生し、その電圧によってアーマチュアの移動を阻害する逆起電力電流が発生します。
これまでの研究では、アクチュエータのアーマチュアの動きに伴う渦電流の効果が考慮されていませんでした。しかし、渦電流がアーマチュアの性能に及ぼす影響が重要になるにつれ、上に挙げたすべての効果が考慮され、計算されて、モデルでの検討対象となっています。このような経緯から、当社のモデルでは、アクチュエータが実際に示す動作を試作前の段階できわめて正確に予測します。このモデルを敏感な解析に使用することで、設計時間短縮とコスト低減を実現でき、技術的にも経済的にも最適なソリューションが得られます。次のセクションで、この手法とその結果について詳しく説明します。
解決方法と結果
静的解析
ここで取り上げる電磁アクチュエータとして提案する構造を図 1 に示します。
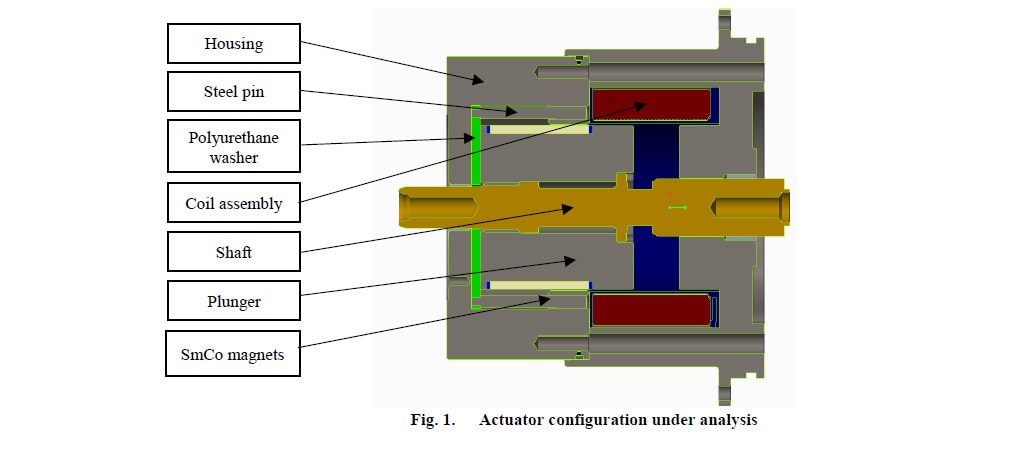
一般的なアクチュエータ (普通は開路コイルと閉路コイルで構成) と構造を比較すると、このタイプのアクチュエータは、ハウジング (フレーム)、鋼製ピン、コイル アセンブリ (コイルとボビン)、アーマチュア (プランジャー)、シャフト、ポリウレタン ワッシャ、永久 SmCo (サマリウム コバルト) マグネット (PM) で構成されています。
コイル巻線の両端に電流を印加すると電磁界が形成されます。このコイルの目的は、アーマチュアを閉路位置まで駆動し、そこに保持することにあります。このアクチュエータは、コイルへの電力が失われると安全な方向 (開路状態) に動作するフェイルセーフとする必要があります。この開路プロセスは、コイルの電流が遮断されると始まり、機械的手段 (スプリングなど) で
完了します。このように、このタイプのアクチュエータでは、これまで一般的だったアクチュエータよりも電力損失が著しく少なく (現代の列車では重要です)、同時に安全性も重視されています。
ステータには磁界が集中します。ステータはコイルの外側を囲むように設けられ、低炭素鋼 AISI (米国鉄鋼協会) 1018 を材料としています。電磁アクチュエータのほとんどで低炭素鋼が使用されています。この材料は高い導磁率を持ち、比較的低コストです。[12]
マグネットは保持力を生成しますが、その強さはハウジングに対するアーマチュアの相対的な位置 (マグネットのリラクタンスの高低) で異なります。
解析の目的上、マグネットの磁界の物理を選択しています。炭素鋼の非線形な磁気特性とマグネットの残留磁束密度を定義するために、関連性のある領域にアンペールの法則を適用します。非線形な磁気特性は、磁気飽和 (印加する外部磁場 H を強くしても、材料の磁化がそれ以上進まなくなる状態) を
考慮するために導入します。[2] [3]
アーマチュアの電磁気力を計算するために、マクスウェルの応力テンソルの手法を応用しています。このテンソルを数学的に表現すると、対象領域を囲む閉じたパス (2 次元の場合) または閉じた表面積 ”A" (3 次元の場合) に沿った積分です。この手法の制限事項として、磁気材料どうしの境界 (極として機能) がある場合、それらの間にきわめて狭い空隙 (0.1 mm 未満) を維持する必要があります。そのようにしないと、きわめて弱い力が算出され、実際の値から乖離した結果になります。[12] [5]
動的解析
アクチュエータが示す動的挙動を調べるために、2 つのモデルでアクチュエータの開路性能と閉路性能を考慮したシミュレーションを進めてきました。[4] [7] [8] このアクチュエータを駆動する電気回路を以下の図 (図 2) に示します。
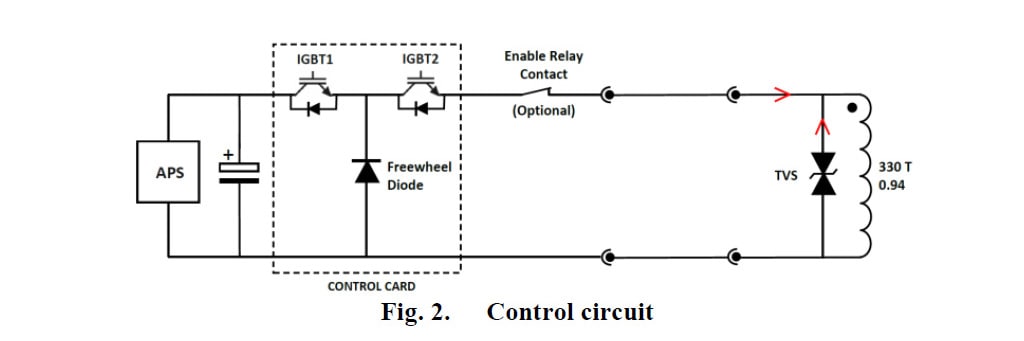
開路動作の場合は、コイルに流れる電流を遮断し、TVS を使用して誘導電圧 (およびそれに起因する誘導電流) を抑制します。閉路動作の場合は、APS (アクチュエータ電源) からのパルス列を使用してアクチュエータを駆動します。
この動作の方程式を次のように解くことができます ((1) ~ (3))。
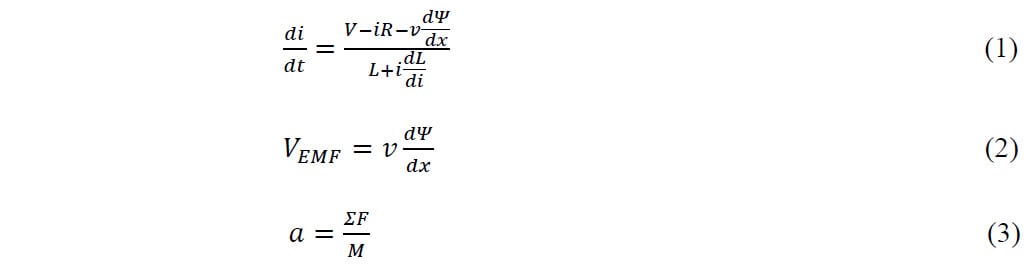
V: 電圧 (V)、i: 電流 (A)、R: 抵抗 (Ω)、L: インダクタンス (H)、VEMF: 逆起 EMF 電圧 (V)、v: 速度 (m/s)、a: 加速度 (m/s2)、t: 時間 (s)、ΣF: 合力 (N)、M: 質量 (kg)、φ: 鎖交磁束 (Wb-T)鎖交磁束には 2 つの成分があり、1 つは PM (BPM) によって形成される磁界に依存しない成分で、もう 1 つはコイル (Bc) によって形成される磁界に起因する成分です。
渦電流は、次の方程式で算出されます。[1]
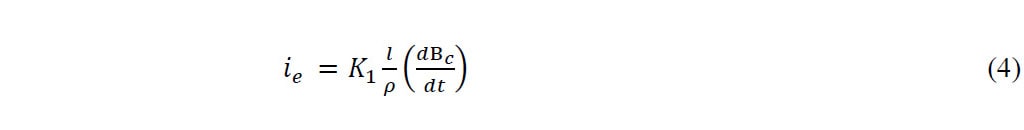
ここで、K1 は幾何学的因子、l はプランジャーの長さ、ρ は材料の抵抗率です。[1] プランジャーを円筒形と仮定すると、方程式 4 は次のようになります。

渦電流によって形成される磁界 (Be) とそれに対応する力 (Fe) は、次の方程式 6 と 7 を使用して算出されます。
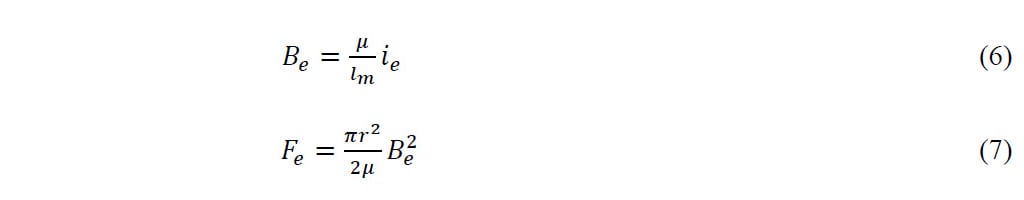
ここで、lm は磁路、r はプランジャーの半径、µ は材料の誘電率です。
シミュレーション結果
さまざまな位置の磁界分布を図 3 に示します。
アーマチュアに近い位置 (図 3a) では、鋼製ハウジングに沿ったアーマチュア部分で磁気抵抗が低い磁路が形成され、上部の大きな空隙で磁気抵抗が高い磁路が発生しています。したがって、ほとんどの磁力線は、ハウジングと接触しているアーマチュア端部を経由して通ります。この位置でマグネットによって形成される保持力は
高い値を示します。フェールセーフ動作を実現するには、アーマチュアを閉路位置に保持するために、同じくこのコイルを使用してより高い保持力を形成します。
開路するために、コイルを流れる電流を遮断すると、アーマチュアが動き始めます。アーマチュアが閉路位置から開路位置へ移動するに伴い、開路位置の空隙が小さくなっていく (磁気抵抗が低くなっていく) ので、閉路状態では磁気抵抗が低かった磁路 (図 3b) の方向へ磁力線が押されます。したがって、プランジャーの底部では保持力が減少し、上部では吸引力が増加します。
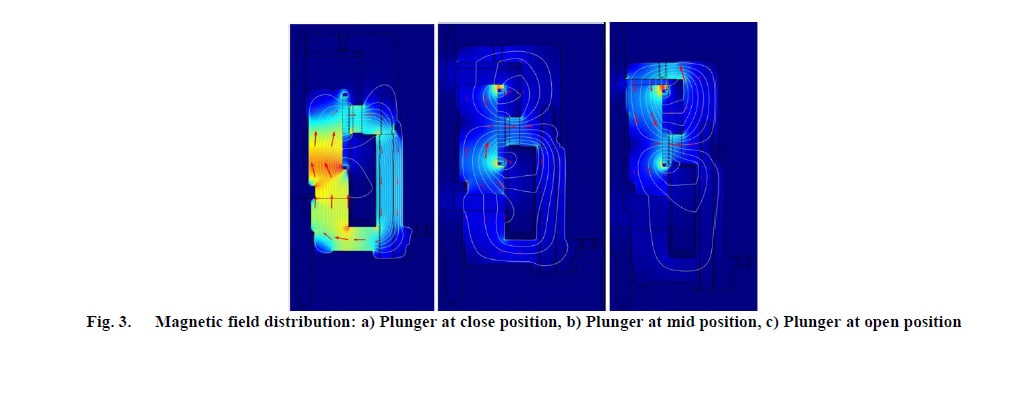
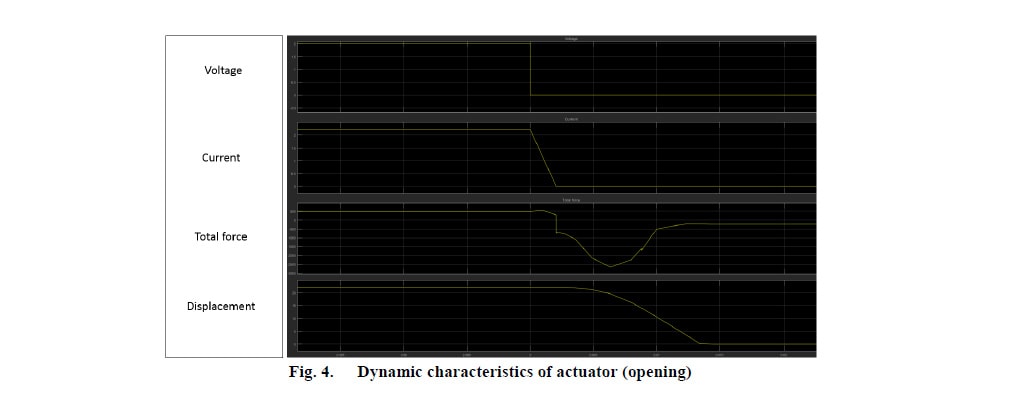
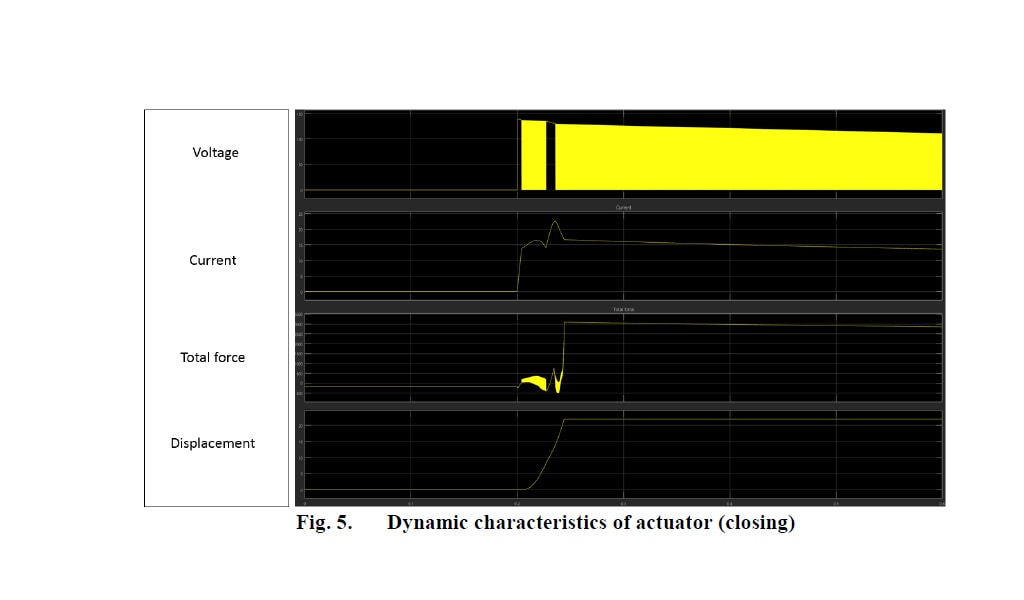
アーマチュアが開路位置に達すると (図 3c)、磁路の磁気抵抗の状態がそれまでとは逆になるので、磁力線はほとんどプランジャー上部に集中します。ここで見られるように、アーマチュアが閉路位置にあるときと開路位置にあるときとでは、磁力線の集中状態が異なります。したがって、開路位置での保持力は、閉路位置での保持力よりも弱くなります。この動的解析の結果を図 4 と図 5 に示します。
わずかに異なるアクチュエータ モデル (最終的な調整を適用する前の設計) を使用したいくつかの予備実験結果 (図 6 と図 7) から、ここで提案した設計と制御回路の概念を実証しています。
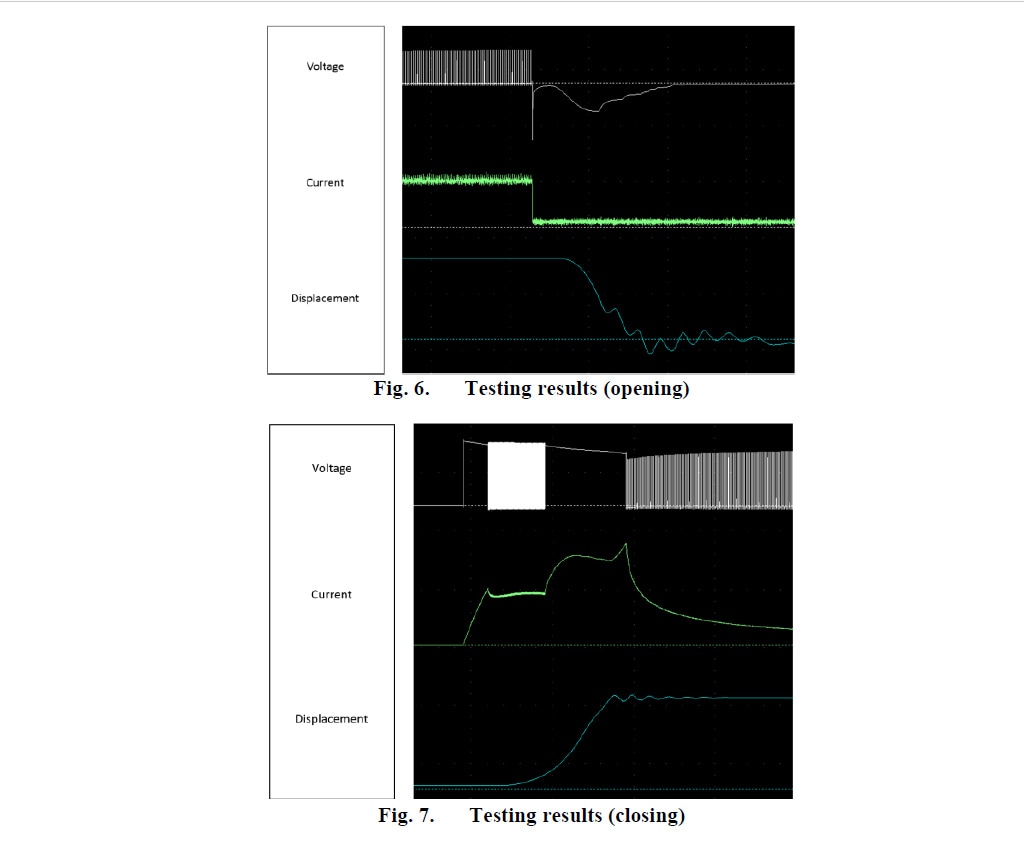
試験で確認された動的特性のプロファイルは、シミュレーション結果と一致しています。閉路動作と開路動作における速度と時間の値は、試験結果とシミュレーション結果でほとんど同じです (両者の差異は 10% 未満)。
考察および要点
アクチュエータの最適化モデルは、誘導に起因して電磁的に発生するブレーキ効果の最小限化または排除を目的として提案されています。開路動作では、新たな制御回路を使用してこの効果を抑制し、閉路動作では、パルス列を導入してアクチュエータの性能を制御します。
システムの効率と性能の向上 (低消費電力) に効果のある革新的なアクチュエータ設計と制御回路は、TE で進めている新世代列車屋根上システムの開発に大きく貢献します。このアクチュエータは、信頼性に優れた動作を実現するために設計され、市場が求めるロー プロファイルと軽量性に対する
要件 (空力性能の改善) および最小限の消費電力に適合しています。
ここでは、試験結果とシミュレーション結果との比較に基づき、提案した計算方法で電磁アクチュエータの過渡特性を正確に解析できるという結論が得られました。また、渦電流による影響は、その形態が複雑であることから既存の各種資料の大半では取り上げられてきませんでした。このレポートでは、この影響を考慮している点も
特筆に値します。したがって、この方法で重要な点は、試作前の段階でこの方法を使用することで、設計と製造に要する時間、コスト、リソースを大幅に削減できることにあります。
謝辞
本プロジェクト全体を通じ、Graham Mcdonald、Robert Phillpotts、Thomas Moore の各氏からいただいたあらゆる支援と専門的な助言に感謝いたします。3 氏からは、機械力の解析とデータから得られた推奨事項に従い、力学モデルと電子回路構成をご提供いただきました。
参考文献
[1] Mandache, L.; D. Topan; K. Al Haddad.“Modeling of Non-Linear Ferromagnetic Cores”.Revue Roumaine de Sciences Techniques.Serie Electrotechnique et Energetique.Vol. 53, Issue 4. 2008.
[2] K. Srairi and M. Feliachi, “Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators,” IEEE Transactions on Magnetics, vol. 34, no. 5, pp. 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov and D. Dimitrov, “Dynamic characteristics of a permanent magnet electromagnetic valve actuator,” in 12th International Conference on Optimization of Electrical and Electronic Equipment, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov and K. Hinov, “Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator,” Elec.Energ., vol. 23, no. 1, pp. 37-43, 2010.
[5] I. Yatchev and E. Ritchie, “Simulation of Dynamics of a Permanent Manget Linear Actuator,” Internation Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, no. 6, pp. 726-730, 2010.
[6] S.-M.Wang, T. Miyano and M. Hubbard, “Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator” IEEE Transactions on Magnetics, vol. 29, no. 2, pp. 1741-1746, 1993.
[7] A. Radulian and N. Mocioi, “Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors”.International Conference and Exposition on Electrical and Power Engineering, Iasi, Romania, 2014.
[8] N. Paudel, “Part 1: How to Model a Linear Electromagnetic Plunger,” 7th June 2016. [Online].Available: https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, “Part 2: Model a Linear Electromagnetic Plunger with a Blocker,” 14th June 2016. [Online].Available: https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer and B. Ulrych, “Electromechanical Actuators Dynamics” J. of Electrical Engineering, vol. 60, no. 5, pp. 255, 2009.
[11] H. Musaab, “Using Look-up Tables to Model an Electromagnetic Suspansion System,” American Journal of Applied Sciences , vol. 9, no. 8, pp. 1199-1202, 2012.
[12] O. Vogel and J. Ulm, “Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics,” in Comsol Conference, Stuttgart, 2011.
FEA による線形電磁アクチュエータの解析
要約
本ホワイトペーパーでは、真空遮断器に使用する電磁アクチュエータの動的特性を解析します。磁気的現象、電気的現象、機械的現象を同時に解析して、アクチュエータの動的な動作を把握します。有限要素解析 (FEA) を使用して磁気パラメータを計算し、その結果を動的解析ソフトウェアにインポートして電気的方程式と機械的方程式を計算します。その解析結果をいくつかの実験データとともに提示します。この技法は、センサ、リレー、スイッチなど他のアクチュエータ システムの動的な電磁動作をきわめて正確に解析する際に使用できます。
問題の提示
電磁アクチュエータは回路ブレーカで広く使用されています。その役割は、真空ボトル中の可動接点が特定の速度と正確な軌道で動作できるようにすることにあります。
このレポートでは、TE の新世代鉄道車両屋根上システムに使用する線形アクチュエータの新たなモデルを提案し、解析します。このアクチュエータの動作に著しく影響する要因はマグネットの抗力です。この力は次の原因で発生します。
- 静的磁界: アーマチュアが動作するときは、それに磁気的吸引力が働いています。この吸引力は、マグネットの位置に応じて、マグネットとアーマチュアとの間で発生する相対的運動に起因しています。
- コイル残留電流: コイルへの保持電圧供給を停止しても、コイル電流がゼロに低下するにはわずかな時間を要します。電流が残留している間は、閉路位置へ接点を引っ張る磁力が生成されます。この電流を迅速に抑制するには次の手段があります。
o TVS (過渡電圧抑制) 電圧を高くする
o コイルのインダクタンスを少なくする
- 誘導される渦電流 [1]
- 運動によって誘導される渦電流: エネルギ損失のほとんどはこの効果が占めており (アーマチュアとマグネットの間で相対的な運動が発生する場合)、アーマチュアの中をマグネットが移動する構造にすること (あるいは、磁界強度が低いマグネットを使用すること、またはこの両方の方法をとること) により、効果的に低減または排除できます。[1]
- 逆起電力 (起電力) による電流: アーマチュアが移動すると逆起電力による電圧が発生し、その電圧によってアーマチュアの移動を阻害する逆起電力電流が発生します。
これまでの研究では、アクチュエータのアーマチュアの動きに伴う渦電流の効果が考慮されていませんでした。しかし、渦電流がアーマチュアの性能に及ぼす影響が重要になるにつれ、上に挙げたすべての効果が考慮され、計算されて、モデルでの検討対象となっています。このような経緯から、当社のモデルでは、アクチュエータが実際に示す動作を試作前の段階できわめて正確に予測します。このモデルを敏感な解析に使用することで、設計時間短縮とコスト低減を実現でき、技術的にも経済的にも最適なソリューションが得られます。次のセクションで、この手法とその結果について詳しく説明します。
解決方法と結果
静的解析
ここで取り上げる電磁アクチュエータとして提案する構造を図 1 に示します。

一般的なアクチュエータ (普通は開路コイルと閉路コイルで構成) と構造を比較すると、このタイプのアクチュエータは、ハウジング (フレーム)、鋼製ピン、コイル アセンブリ (コイルとボビン)、アーマチュア (プランジャー)、シャフト、ポリウレタン ワッシャ、永久 SmCo (サマリウム コバルト) マグネット (PM) で構成されています。
コイル巻線の両端に電流を印加すると電磁界が形成されます。このコイルの目的は、アーマチュアを閉路位置まで駆動し、そこに保持することにあります。このアクチュエータは、コイルへの電力が失われると安全な方向 (開路状態) に動作するフェイルセーフとする必要があります。この開路プロセスは、コイルの電流が遮断されると始まり、機械的手段 (スプリングなど) で
完了します。このように、このタイプのアクチュエータでは、これまで一般的だったアクチュエータよりも電力損失が著しく少なく (現代の列車では重要です)、同時に安全性も重視されています。
ステータには磁界が集中します。ステータはコイルの外側を囲むように設けられ、低炭素鋼 AISI (米国鉄鋼協会) 1018 を材料としています。電磁アクチュエータのほとんどで低炭素鋼が使用されています。この材料は高い導磁率を持ち、比較的低コストです。[12]
マグネットは保持力を生成しますが、その強さはハウジングに対するアーマチュアの相対的な位置 (マグネットのリラクタンスの高低) で異なります。
解析の目的上、マグネットの磁界の物理を選択しています。炭素鋼の非線形な磁気特性とマグネットの残留磁束密度を定義するために、関連性のある領域にアンペールの法則を適用します。非線形な磁気特性は、磁気飽和 (印加する外部磁場 H を強くしても、材料の磁化がそれ以上進まなくなる状態) を
考慮するために導入します。[2] [3]
アーマチュアの電磁気力を計算するために、マクスウェルの応力テンソルの手法を応用しています。このテンソルを数学的に表現すると、対象領域を囲む閉じたパス (2 次元の場合) または閉じた表面積 ”A" (3 次元の場合) に沿った積分です。この手法の制限事項として、磁気材料どうしの境界 (極として機能) がある場合、それらの間にきわめて狭い空隙 (0.1 mm 未満) を維持する必要があります。そのようにしないと、きわめて弱い力が算出され、実際の値から乖離した結果になります。[12] [5]
動的解析
アクチュエータが示す動的挙動を調べるために、2 つのモデルでアクチュエータの開路性能と閉路性能を考慮したシミュレーションを進めてきました。[4] [7] [8] このアクチュエータを駆動する電気回路を以下の図 (図 2) に示します。

開路動作の場合は、コイルに流れる電流を遮断し、TVS を使用して誘導電圧 (およびそれに起因する誘導電流) を抑制します。閉路動作の場合は、APS (アクチュエータ電源) からのパルス列を使用してアクチュエータを駆動します。
この動作の方程式を次のように解くことができます ((1) ~ (3))。
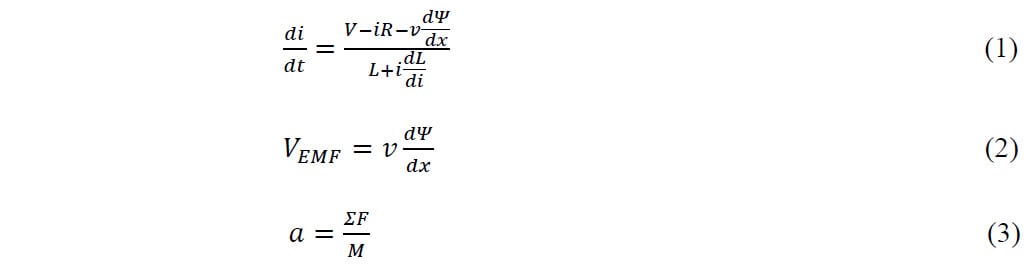
V: 電圧 (V)、i: 電流 (A)、R: 抵抗 (Ω)、L: インダクタンス (H)、VEMF: 逆起 EMF 電圧 (V)、v: 速度 (m/s)、a: 加速度 (m/s2)、t: 時間 (s)、ΣF: 合力 (N)、M: 質量 (kg)、φ: 鎖交磁束 (Wb-T)鎖交磁束には 2 つの成分があり、1 つは PM (BPM) によって形成される磁界に依存しない成分で、もう 1 つはコイル (Bc) によって形成される磁界に起因する成分です。
渦電流は、次の方程式で算出されます。[1]
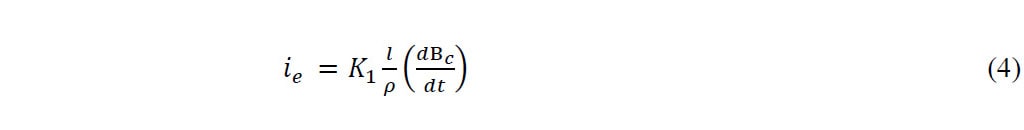
ここで、K1 は幾何学的因子、l はプランジャーの長さ、ρ は材料の抵抗率です。[1] プランジャーを円筒形と仮定すると、方程式 4 は次のようになります。

渦電流によって形成される磁界 (Be) とそれに対応する力 (Fe) は、次の方程式 6 と 7 を使用して算出されます。
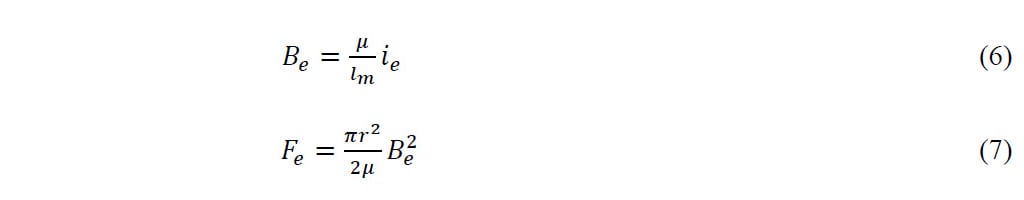
ここで、lm は磁路、r はプランジャーの半径、µ は材料の誘電率です。
シミュレーション結果
さまざまな位置の磁界分布を図 3 に示します。
アーマチュアに近い位置 (図 3a) では、鋼製ハウジングに沿ったアーマチュア部分で磁気抵抗が低い磁路が形成され、上部の大きな空隙で磁気抵抗が高い磁路が発生しています。したがって、ほとんどの磁力線は、ハウジングと接触しているアーマチュア端部を経由して通ります。この位置でマグネットによって形成される保持力は
高い値を示します。フェールセーフ動作を実現するには、アーマチュアを閉路位置に保持するために、同じくこのコイルを使用してより高い保持力を形成します。
開路するために、コイルを流れる電流を遮断すると、アーマチュアが動き始めます。アーマチュアが閉路位置から開路位置へ移動するに伴い、開路位置の空隙が小さくなっていく (磁気抵抗が低くなっていく) ので、閉路状態では磁気抵抗が低かった磁路 (図 3b) の方向へ磁力線が押されます。したがって、プランジャーの底部では保持力が減少し、上部では吸引力が増加します。

アーマチュアが開路位置に達すると (図 3c)、磁路の磁気抵抗の状態がそれまでとは逆になるので、磁力線はほとんどプランジャー上部に集中します。ここで見られるように、アーマチュアが閉路位置にあるときと開路位置にあるときとでは、磁力線の集中状態が異なります。したがって、開路位置での保持力は、閉路位置での保持力よりも弱くなります。この動的解析の結果を図 4 と図 5 に示します。


わずかに異なるアクチュエータ モデル (最終的な調整を適用する前の設計) を使用したいくつかの予備実験結果 (図 6 と図 7) から、ここで提案した設計と制御回路の概念を実証しています。

試験で確認された動的特性のプロファイルは、シミュレーション結果と一致しています。閉路動作と開路動作における速度と時間の値は、試験結果とシミュレーション結果でほとんど同じです (両者の差異は 10% 未満)。
考察および要点
アクチュエータの最適化モデルは、誘導に起因して電磁的に発生するブレーキ効果の最小限化または排除を目的として提案されています。開路動作では、新たな制御回路を使用してこの効果を抑制し、閉路動作では、パルス列を導入してアクチュエータの性能を制御します。
システムの効率と性能の向上 (低消費電力) に効果のある革新的なアクチュエータ設計と制御回路は、TE で進めている新世代列車屋根上システムの開発に大きく貢献します。このアクチュエータは、信頼性に優れた動作を実現するために設計され、市場が求めるロー プロファイルと軽量性に対する
要件 (空力性能の改善) および最小限の消費電力に適合しています。
ここでは、試験結果とシミュレーション結果との比較に基づき、提案した計算方法で電磁アクチュエータの過渡特性を正確に解析できるという結論が得られました。また、渦電流による影響は、その形態が複雑であることから既存の各種資料の大半では取り上げられてきませんでした。このレポートでは、この影響を考慮している点も
特筆に値します。したがって、この方法で重要な点は、試作前の段階でこの方法を使用することで、設計と製造に要する時間、コスト、リソースを大幅に削減できることにあります。
謝辞
本プロジェクト全体を通じ、Graham Mcdonald、Robert Phillpotts、Thomas Moore の各氏からいただいたあらゆる支援と専門的な助言に感謝いたします。3 氏からは、機械力の解析とデータから得られた推奨事項に従い、力学モデルと電子回路構成をご提供いただきました。
参考文献
[1] Mandache, L.; D. Topan; K. Al Haddad.“Modeling of Non-Linear Ferromagnetic Cores”.Revue Roumaine de Sciences Techniques.Serie Electrotechnique et Energetique.Vol. 53, Issue 4. 2008.
[2] K. Srairi and M. Feliachi, “Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators,” IEEE Transactions on Magnetics, vol. 34, no. 5, pp. 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov and D. Dimitrov, “Dynamic characteristics of a permanent magnet electromagnetic valve actuator,” in 12th International Conference on Optimization of Electrical and Electronic Equipment, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov and K. Hinov, “Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator,” Elec.Energ., vol. 23, no. 1, pp. 37-43, 2010.
[5] I. Yatchev and E. Ritchie, “Simulation of Dynamics of a Permanent Manget Linear Actuator,” Internation Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, no. 6, pp. 726-730, 2010.
[6] S.-M.Wang, T. Miyano and M. Hubbard, “Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator” IEEE Transactions on Magnetics, vol. 29, no. 2, pp. 1741-1746, 1993.
[7] A. Radulian and N. Mocioi, “Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors”.International Conference and Exposition on Electrical and Power Engineering, Iasi, Romania, 2014.
[8] N. Paudel, “Part 1: How to Model a Linear Electromagnetic Plunger,” 7th June 2016. [Online].Available: https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, “Part 2: Model a Linear Electromagnetic Plunger with a Blocker,” 14th June 2016. [Online].Available: https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer and B. Ulrych, “Electromechanical Actuators Dynamics” J. of Electrical Engineering, vol. 60, no. 5, pp. 255, 2009.
[11] H. Musaab, “Using Look-up Tables to Model an Electromagnetic Suspansion System,” American Journal of Applied Sciences , vol. 9, no. 8, pp. 1199-1202, 2012.
[12] O. Vogel and J. Ulm, “Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics,” in Comsol Conference, Stuttgart, 2011.
