Analyse des linearen elektromagnetischen Antriebs mit FEM
AUSZUG
In diesem Bericht haben wir die dynamischen Eigenschaften eines elektromagnetischen Antriebs analysiert, der für Vakuumleistungsschalter verwendet wird. Die magnetischen, elektrischen und mechanischen Phänomene werden gleichzeitig analysiert, um das dynamische Verhalten des Antriebs zu ermitteln. Die magnetischen Parameter werden mithilfe der Finite-Elemente-Methode (FEM) berechnet und dann in eine dynamische Analysesoftware importiert, welche die elektrischen und mechanischen Gleichungen berechnet. Die Analyseergebnisse werden zusammen mit einigen experimentellen Daten dargestellt. Dieses Verfahren kann verwendet werden, um das dynamische elektromagnetische Verhalten von Sensoren, Relais, Schaltern und anderen Antriebssystemen sehr genau zu analysieren.
PROBLEMSTELLUNG
Der elektromagnetische Antrieb wird häufig in Leistungsschaltern genutzt. Seine Aufgabe ist es, die Bewegung der beweglichen Kontakte der Vakuumflasche mit bestimmten Geschwindigkeiten und präzisen Bewegungsbahnen zu erreichen.
In diesem Bericht wird ein neuartiges Modell eines linearen Antriebs vorgeschlagen und analysiert, das in der neuen Generation der Schienenfahrzeug-Fahrleitungssysteme von TE zum Einsatz kommen wird. Ein Faktor, der die Funktionsweise des Antriebs wesentlich beeinflusst, ist die magnetische Zugkraft. Diese Kraft kann auf Folgendes zurückzuführen sein:
- Statisches Magnetfeld: Während sich der Anker bewegt, erfährt er eine magnetische Anziehungskraft (aufgrund der relativen Bewegung mit den Magneten je nach Position).
- Spulenreststrom: Wenn die Haltespannung von der Spule getrennt wird, braucht es einige Zeit, bis der Spulenstrom auf Null abfällt. Ist er vorhanden, erzeugt er eine magnetischen Anziehungskraft in Richtung der Schließposition. Ein schneller Stromabfall kann durch Folgendes erreicht werden:
o Zunehmende TVS-Spannung (Transient Voltage Suppressor)
o Abnehmende Spuleninduktivität
- Induzierte Wirbelströme [1]
- Bewegungsinduzierte Wirbelströme: Dieser Effekt macht den größten Teil der Energieverluste aus (wenn es eine relative Bewegung zwischen dem Anker und den Magneten gibt) und kann effektiv reduziert oder sogar eliminiert werden, indem die Magnete im Anker bewegt werden (und/oder Magnete mit verminderter Magnetfeldstärke verwendet werden) [1].
- EMK-Gegenstrom (elektromotorische Kraft): Die Bewegung des Ankers verursacht EMK-Gegenspannung, die wiederum zu EMK-Strom führt, welcher der Bewegung entgegen wirkt.
In der bisherigen Forschung wird die Wirkung der Wirbelströme in der Bewegung des Antriebsankers nicht berücksichtigt. Da dies jedoch wichtig für die Leistung des Antriebs ist, wurden alle oben genannten Effekte berücksichtigt, berechnet und in das Modell aufgenommen. Daher sagt unser Modell das tatsächliche Verhalten des Antriebs vor dem Prototyping mit hoher Genauigkeit voraus und kann für die Sensitivitätsanalyse verwendet werden, um die Zeit für das Design sowie die Kosten zu reduzieren und eine optimale technische und wirtschaftliche Lösung bereitzustellen. Die nächsten Abschnitte erhalten eine ausführliche Beschreibung der Methoden und Ergebnisse.
METHODEN UND ERGEBNISSE
Statische Analyse
Abbildung 1 zeigt den vorgeschlagenen Aufbau des elektromagnetischen Antriebs:
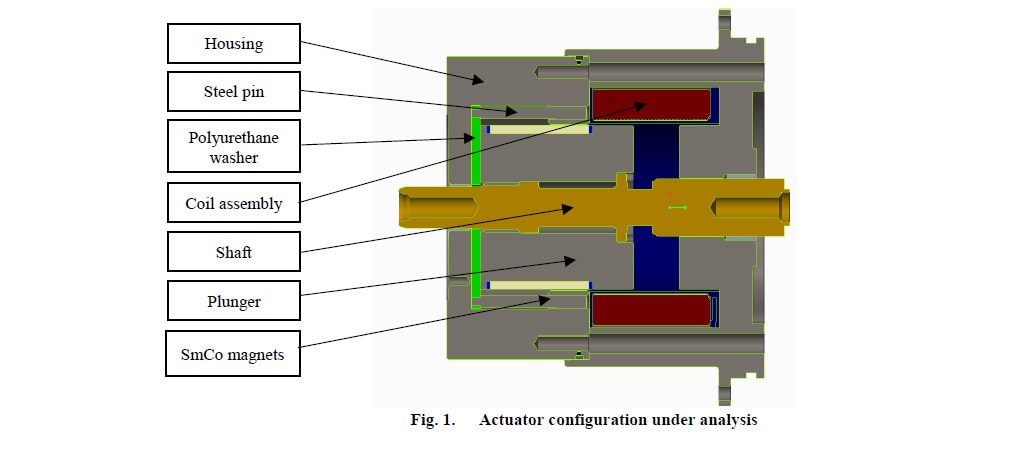
Im Gegensatz zu einem typischen Antrieb (der in der Regel eine Öffnungs- und eine Schließspule umfasst) besteht diese Art von Antrieb aus dem Gehäuse (oder Gestell), dem Stahlstift, der Spulenbaugruppe (Spule/Spulenkern), dem Anker (Kolben), der Welle, der Unterlegscheibe aus Polyurethan sowie den Dauermagneten (PM) aus Samarium-Cobalt (SmCo).
Die Spulenwicklungen erzeugen ein elektromagnetisches Feld, wenn der Strom über ihre Anschlüsse angelegt wird. Der Zweck der Spule ist es, den Anker in die Schließposition zu steuern und ihn dort zu halten. Im Falle eines Stromverlusts in der Spule sollte der Antrieb ausfallsicher (geöffnet) sein. Der Öffnungsprozess beginnt, wenn der Strom in der Spule unterbrochen wird, und wird nur mit
mechanischen Mitteln (Federn usw.) erreicht. Daher ist die Verlustleistung (kritisch für moderne Züge) in dieser Art von Antrieb deutlich geringer als die Verlustleistung in einem typischen Antrieb, während die Sicherheit im Vordergrund steht.
Der Stator bündelt das Magnetfeld. Er umgibt die Spule außen und besteht aus AISI-Stahl (American Iron and Steel Institute) 1018 mit niedrigem Kohlenstoffgehalt. Stahl mit niedrigem Kohlenstoffgehalt wird für die meisten elektromagnetischen Antriebe verwendet. Es weist eine hohe Durchlässigkeit auf und ist relativ kostengünstig [12].
Die Magnete erzeugen eine Haltekraft, die von der Position des Ankers im Verhältnis zum Gehäuse abhängt (geringer und hoher magnetischer Widerstand).
Für die Analyse wurde die Magnetfeldphysik ausgewählt. Um die nichtlinearen magnetischen Eigenschaften des Kohlenstoffstahls und die remanente Flussdichte der Magnete zu definieren, wurde das Ampèresche Gesetz auf die relevanten Bereiche angewendet. Die nichtlinearen magnetischen Eigenschaften werden eingeführt, um die magnetische Sättigung (der Zustand, in dem die Magnetisierung eines
Materials einen Punkt erreicht, an dem sie aufgrund des externen angewendeten Magnetfeldes H nicht weiter zunehmen kann) [2] [3].
Für die Berechnung der elektromagnetischen Kraft im Anker wurde die Methode des Maxwellschen Spannungstensors angewendet. Dieser Tensor ist mathematisch ein Integral entlang eines abgeschlossenen Weges (in 2D) oder einer abgeschlossenen Oberfläche „A“ (in 3D) um einen Bereich von Interesse. Eine der Einschränkungen dieser Methode besteht darin, dass zwischen einem magnetischen Material und einer magnetischen Materialschnittstelle (Pole) ein sehr kleiner Luftspalt (< 0,1 mm) aufrechterhalten werden muss. Andernfalls wird ein sehr niedriger Kraftwert berechnet, der nicht dem realen Wert entspricht [12] [5].
Dynamische Analyse
Zur Untersuchung des dynamischen Verhaltens des Antriebs wurden zwei Modelle simuliert, um die Öffnungs- und Schließleistung zu berücksichtigen [4] [7] [8]. Der Stromkreis, mit dem der Antrieb betrieben wird, wird unten dargestellt (Abbildung 2):
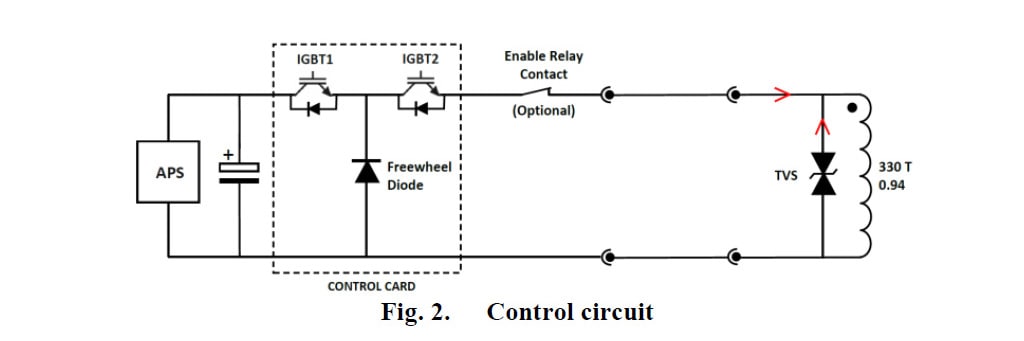
Beim Öffnen wird der Strom in der Spule abgeschaltet. Dann wird die induzierte Spannung (und damit der induzierte Strom) mit dem TVS unterdrückt. Beim Schließen wird eine Impulssequenz aus der Stromquelle des Antriebs (APS, Actuator Power Source) verwendet, um den Antrieb zu betreiben.
Die gelösten Gleichungen ((1) – (3)) lauten wie folgt:
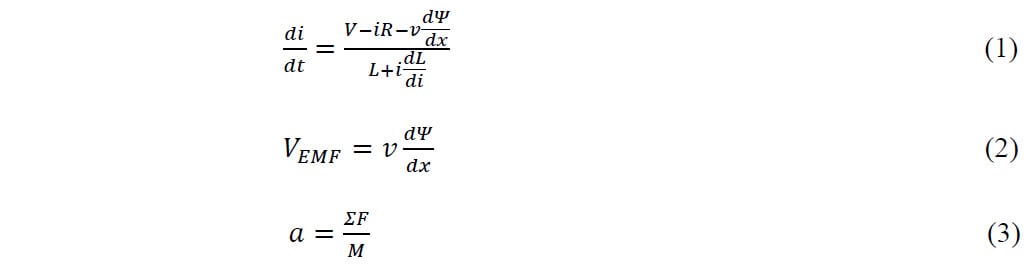
V: Spannung (V), i: Strom (A), R: Widerstand (Ω), L: Induktivität (H), VEMF: EMK-Gegenspannung (V), v: Geschwindigkeit (m/s), α: Beschleunigung (m/s2), t: Zeit (s)ΣF: Gesamtkraft (N), M: Masse (kg), Ψ: Flussverkettung (Wb-T). Die Flussverkettungen bestehen aus zwei Komponenten: Eine Komponenten ist von dem Magnetfeld abhängig, das die Dauermagneten (BPM) erzeugen, und die andere von dem durch die Spule (Bc) erzeugten Magnetfeld.
Die Wirbelströme wurden mit folgender Gleichung berechnet [1]:
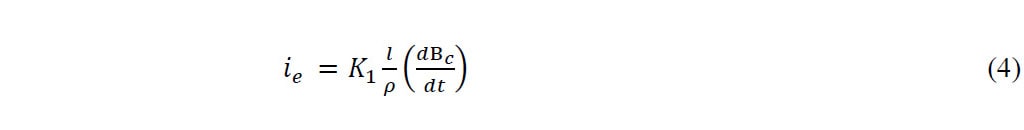
Wobei K1 ein geometrischer Faktor, l die Länge des Kolbens und ρ der spezifische Widerstand des Materials ist [1]. Vorausgesetzt, der Kolben ist ein Zylinder, lautet Gleichung 4 wie folgt:

Das Magnetfeld, das durch die Wirbelströme (Be) und die entsprechende Kraft (Fe) erzeugt wurde, wurde mit Gleichungen 6 und 7 berechnet.
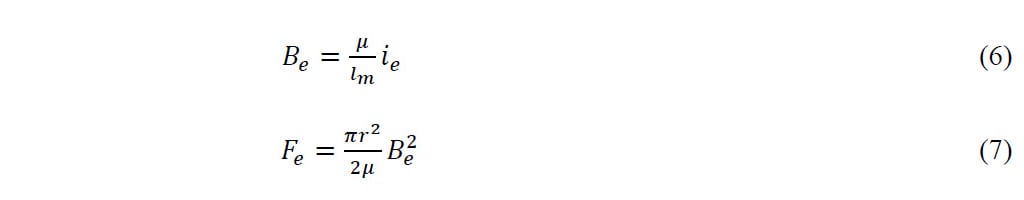
Wobei lm der magnetische Weg, r der Radius des Kolbens und μ die Dielektrizitätskonstante des Materials ist.
Simulationsergebnisse
Die Magnetfeldverteilung in verschiedenen Positionen wird in Abbildung 3 dargestellt.
In der Schließposition (Abbildung 3a) bildet der Anker zusammen mit dem Stahlgehäuse einen Weg mit geringem magnetischen Widerstand, während die große Lücke oben einen Weg mit hohem magnetischen Widerstand darstellt. Daher verlaufen die Magnetfeldlinien fast ausschließlich durch das Ende des Ankers, der Kontakt zum Gehäuse hat. Die Haltekraft, die von den Magneten in dieser
Position erzeugt wird, weist einen hohen Wert auf. Für einen ausfallsicheren Betrieb wird die Spule auch verwendet, um eine noch höhere Haltekraft zu erzeugen und den Anker in der Schließposition zu halten.
Für die Öffnung wird der Strom, der durch die Spule fließt, abgeschaltet, und der Anker bewegt sich. Während der Anker sich von der Schließposition in die Öffnungsposition bewegt, werden die Magnetfeldlinien in Richtung des Weges mit dem zuvor geringeren Widerstand verschoben (Abbildung 3b), da nun der Luftspalt in der Öffnungsposition immer kleiner wird bzw. der magnetische Widerstand abnimmt. Daher nimmt die Haltekraft unten ab, während die Anziehungskraft oben steigt.
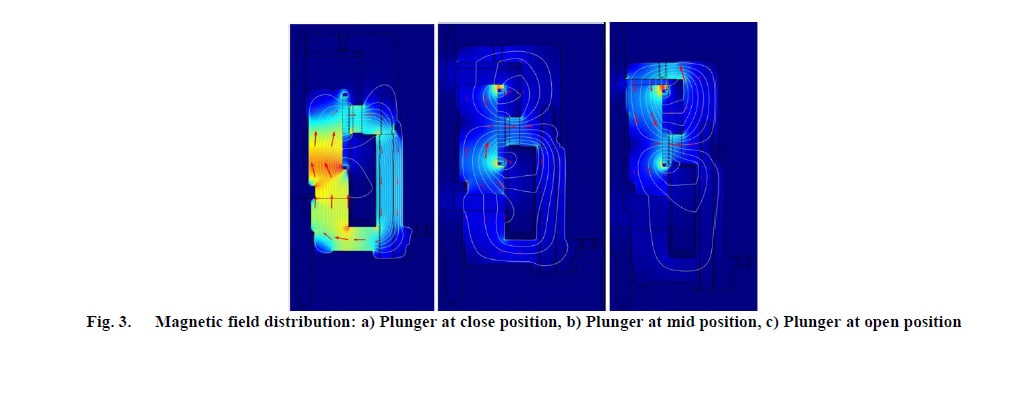
Wenn der Anker die Öffnungsposition erreicht (Abbildung 3c), ist der Widerstandsweg umgekehrt, sodass sich die Magnetfeldlinien hauptsächlich oben konzentrieren. Die Magnetfeldkonzentrationen in der Schließ- und in der Öffnungsposition des Ankers sind also unterschiedlich. Daher weist die Haltekraft in der Öffnungsposition einen niedrigeren Wert auf als in der Schließposition. Die Ergebnisse der dynamischen Analyse werden in den Abbildungen 4 und 5 dargestellt:
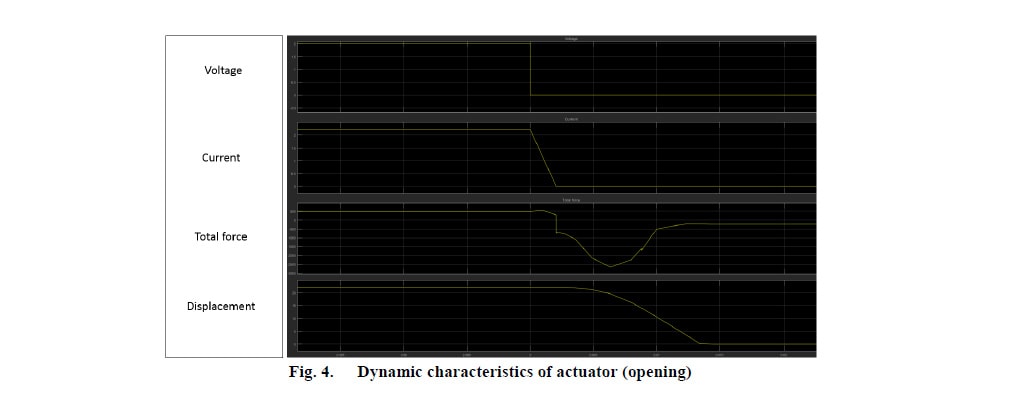
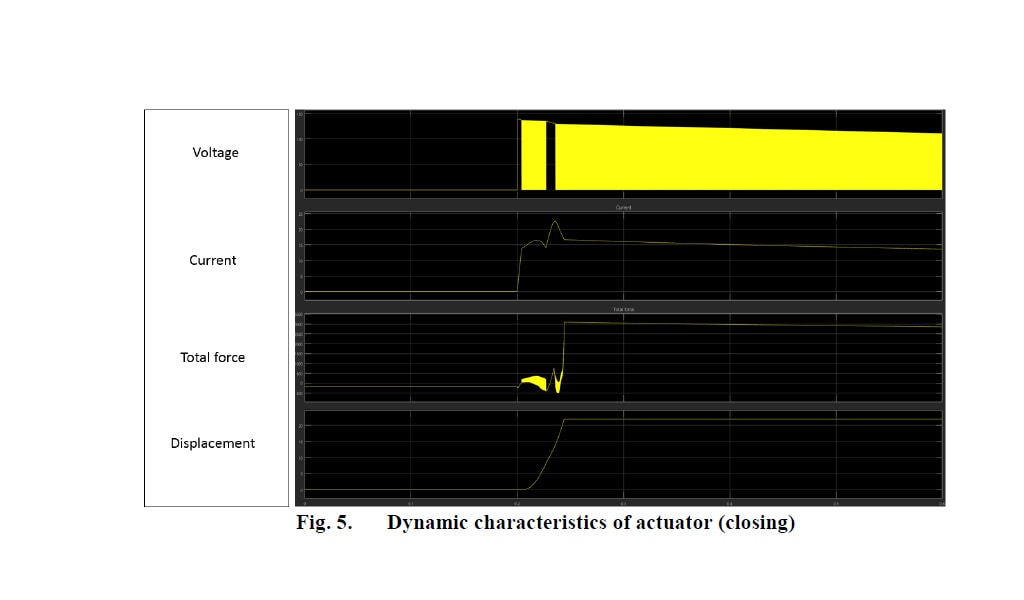
Einige vorläufige experimentelle Ergebnisse (Abbildungen 6 und 7) in leicht unterschiedlichen Antriebsmodellen (Designs vor den endgültigen Anpassungen) belegen das Konzept des vorgeschlagenen Designs und Steuerungskreises.
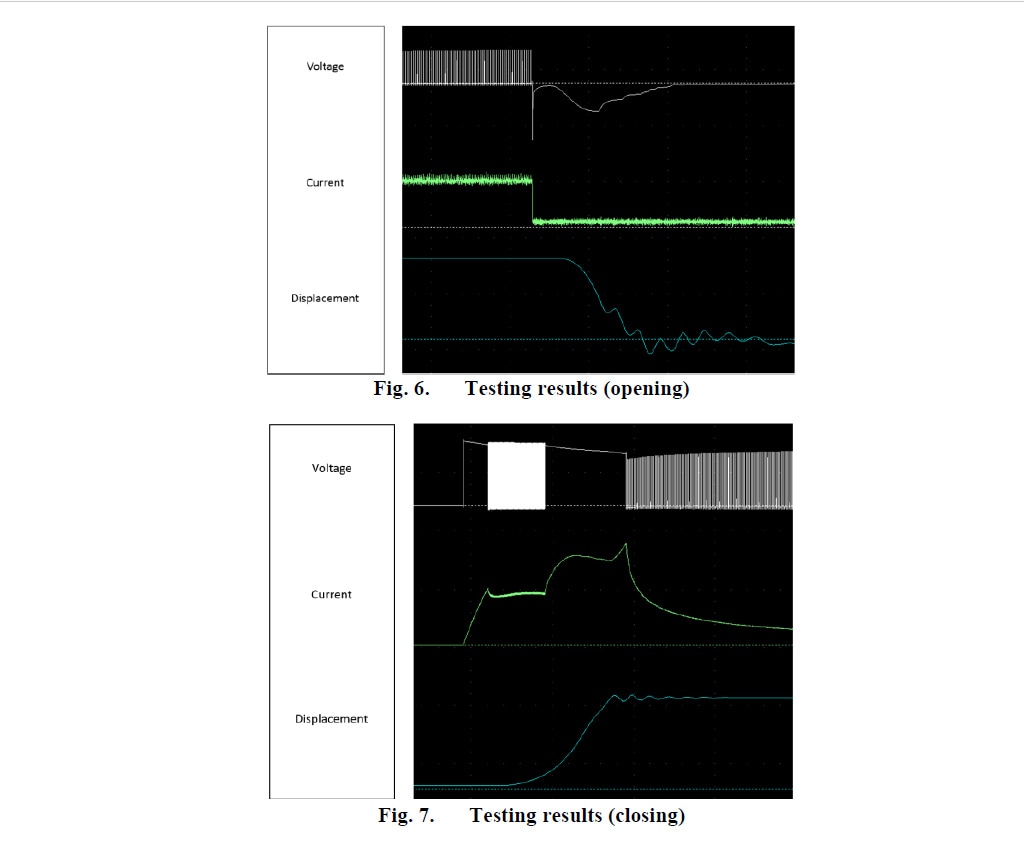
Das Profil der dynamischen Eigenschaften, die bei der Prüfung beobachtet wurden, stimmt mit den Simulationsergebnissen überein. Die Geschwindigkeitswerte und die Dauer des Schließ- und Öffnungsvorgangs sind in Tests und Simulationen ähnlich (Fehlerquote unter 10 %).
ERÖRTERUNG UND KERNASPEKTE
Das optimierte Modell des Antriebs soll die Wirkung der elektromagnetischen Bremsung durch Induktion minimieren oder gar eliminieren. Zur Unterdrückung dieses Effekts beim Öffnen wird ein neuartiger Steuerungskreis verwendet, während beim Schließen eine Impulsfolge induziert wird, um die Leistung des Antriebs zu steuern.
Das innovative Antriebsdesign und der neuartige Steuerungskreis, der die Effizienz und Leistung des Systems verbessert (geringe Verlustleistung), tragen wesentlich zur Weiterentwicklung der neuen Generation der Dachaufbauten von Zügen von TE bei. Der Antrieb ist für zuverlässigen Betrieb ausgelegt und entspricht in Bezug auf sein flaches Profil und seine leichte Bauweise
den Marktanforderungen (Verbesserung der aerodynamischen Leistung). Zudem ist der Stromverbrauch minimal.
Basierend auf dem Vergleich zwischen Test- und Simulationsergebnissen wird der Schluss gezogen, dass die vorgeschlagene Berechnungsmethode die transienten Eigenschaften eines elektromagnetischen Antriebs genau analysieren kann. Es sei darauf hingewiesen, dass in diesem Bericht der Effekt des Wirbelstroms berücksichtigt wird. Aufgrund seiner Komplexität
ist dies in den meisten vorhandenen Berichten nicht der Fall. Daher liegt die Bedeutung dieser Methode darin, dass sie vor dem Prototyping eingesetzt werden kann, um Zeit, Kosten und Ressourcen während der Konstruktion und Fertigung deutlich zu reduzieren.
ANERKENNUNGEN
Wir möchten Graham Mcdonald, Robert Phillpotts und Thomas Moore für die Unterstützung und die kompetente Beratung während des gesamten Projekts danken. Sie stellten die mechanischen Modelle und die Elektronikkonfigurationen nach den Empfehlungen aus der Analyse und den Daten für die mechanischen Kräfte bereit.
VERWEISE
[1] Mandache, L.; D. Topan; K. Al Haddad. „Modeling of Non-Linear Ferromagnetic Cores“. Revue Roumaine de Sciences Techniques. Serie Electrotechnique et Energetique. Band 53, Ausgabe 4. 2008.
[2] K. Srairi und M. Feliachi, „Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators“, IEEE Transactions on Magnetics, Band 34, Nr. 5, Seite 3608–3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov und D. Dimitrov, „Dynamic characteristics of a permanent magnet electromagnetic valve actuator“ in 12th International Conference on Optimization of Electrical and Electronic Equipment, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov und K. Hinov, „Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator“, Elec. Energ., Band 23, Nr. 1, Seite 37–43, 2010.
[5] I. Yatchev und E. Ritchie, „Simulation of Dynamics of a Permanget Linear Actuator“, International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, Band 4, Nr. 6, S. 726–730, 2010.
[6] S.-M. Wang, T. Miyano und M. Hubbard, „Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator“, IEEE Transactions on Magnetics, Band 29, Nr. 2, S. 1741–1746, 1993.
[7] A. Radulian und N. Mocioi, „Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors“. International Conference and Exposition on Electrical and Power Engineering, Iasi, Rumänien, 2014.
[8] N. Paudel, „Part 1: How to Model a Linear Electromagnetic Plunger“, 7. Juni 2016. [Online]. Verfügbar unter https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, „Part 2: Model a Linear Electromagnetic Plunger with a Blocker“, 14. Juni 2016. [Online]. Verfügbar unter https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer und B. Ulrych, „Electromechanical Actuators Dynamics“, J. of Electrical Engineering, Band 60, Nr. 5, S. 255, 2009.
[11] H. Musaab, „Using Look-up Tables to Model an Electromagnetic Suspansion System“, American Journal of Applied Sciences, Band 9, Nr. 8, S. 1199–1202, 2012.
[12] O. Vogel und J. Ulm, „Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics“, COMSOL-Konferenz, Stuttgart, 2011.
Analyse des linearen elektromagnetischen Antriebs mit FEM
AUSZUG
In diesem Bericht haben wir die dynamischen Eigenschaften eines elektromagnetischen Antriebs analysiert, der für Vakuumleistungsschalter verwendet wird. Die magnetischen, elektrischen und mechanischen Phänomene werden gleichzeitig analysiert, um das dynamische Verhalten des Antriebs zu ermitteln. Die magnetischen Parameter werden mithilfe der Finite-Elemente-Methode (FEM) berechnet und dann in eine dynamische Analysesoftware importiert, welche die elektrischen und mechanischen Gleichungen berechnet. Die Analyseergebnisse werden zusammen mit einigen experimentellen Daten dargestellt. Dieses Verfahren kann verwendet werden, um das dynamische elektromagnetische Verhalten von Sensoren, Relais, Schaltern und anderen Antriebssystemen sehr genau zu analysieren.
PROBLEMSTELLUNG
Der elektromagnetische Antrieb wird häufig in Leistungsschaltern genutzt. Seine Aufgabe ist es, die Bewegung der beweglichen Kontakte der Vakuumflasche mit bestimmten Geschwindigkeiten und präzisen Bewegungsbahnen zu erreichen.
In diesem Bericht wird ein neuartiges Modell eines linearen Antriebs vorgeschlagen und analysiert, das in der neuen Generation der Schienenfahrzeug-Fahrleitungssysteme von TE zum Einsatz kommen wird. Ein Faktor, der die Funktionsweise des Antriebs wesentlich beeinflusst, ist die magnetische Zugkraft. Diese Kraft kann auf Folgendes zurückzuführen sein:
- Statisches Magnetfeld: Während sich der Anker bewegt, erfährt er eine magnetische Anziehungskraft (aufgrund der relativen Bewegung mit den Magneten je nach Position).
- Spulenreststrom: Wenn die Haltespannung von der Spule getrennt wird, braucht es einige Zeit, bis der Spulenstrom auf Null abfällt. Ist er vorhanden, erzeugt er eine magnetischen Anziehungskraft in Richtung der Schließposition. Ein schneller Stromabfall kann durch Folgendes erreicht werden:
o Zunehmende TVS-Spannung (Transient Voltage Suppressor)
o Abnehmende Spuleninduktivität
- Induzierte Wirbelströme [1]
- Bewegungsinduzierte Wirbelströme: Dieser Effekt macht den größten Teil der Energieverluste aus (wenn es eine relative Bewegung zwischen dem Anker und den Magneten gibt) und kann effektiv reduziert oder sogar eliminiert werden, indem die Magnete im Anker bewegt werden (und/oder Magnete mit verminderter Magnetfeldstärke verwendet werden) [1].
- EMK-Gegenstrom (elektromotorische Kraft): Die Bewegung des Ankers verursacht EMK-Gegenspannung, die wiederum zu EMK-Strom führt, welcher der Bewegung entgegen wirkt.
In der bisherigen Forschung wird die Wirkung der Wirbelströme in der Bewegung des Antriebsankers nicht berücksichtigt. Da dies jedoch wichtig für die Leistung des Antriebs ist, wurden alle oben genannten Effekte berücksichtigt, berechnet und in das Modell aufgenommen. Daher sagt unser Modell das tatsächliche Verhalten des Antriebs vor dem Prototyping mit hoher Genauigkeit voraus und kann für die Sensitivitätsanalyse verwendet werden, um die Zeit für das Design sowie die Kosten zu reduzieren und eine optimale technische und wirtschaftliche Lösung bereitzustellen. Die nächsten Abschnitte erhalten eine ausführliche Beschreibung der Methoden und Ergebnisse.
METHODEN UND ERGEBNISSE
Statische Analyse
Abbildung 1 zeigt den vorgeschlagenen Aufbau des elektromagnetischen Antriebs:

Im Gegensatz zu einem typischen Antrieb (der in der Regel eine Öffnungs- und eine Schließspule umfasst) besteht diese Art von Antrieb aus dem Gehäuse (oder Gestell), dem Stahlstift, der Spulenbaugruppe (Spule/Spulenkern), dem Anker (Kolben), der Welle, der Unterlegscheibe aus Polyurethan sowie den Dauermagneten (PM) aus Samarium-Cobalt (SmCo).
Die Spulenwicklungen erzeugen ein elektromagnetisches Feld, wenn der Strom über ihre Anschlüsse angelegt wird. Der Zweck der Spule ist es, den Anker in die Schließposition zu steuern und ihn dort zu halten. Im Falle eines Stromverlusts in der Spule sollte der Antrieb ausfallsicher (geöffnet) sein. Der Öffnungsprozess beginnt, wenn der Strom in der Spule unterbrochen wird, und wird nur mit
mechanischen Mitteln (Federn usw.) erreicht. Daher ist die Verlustleistung (kritisch für moderne Züge) in dieser Art von Antrieb deutlich geringer als die Verlustleistung in einem typischen Antrieb, während die Sicherheit im Vordergrund steht.
Der Stator bündelt das Magnetfeld. Er umgibt die Spule außen und besteht aus AISI-Stahl (American Iron and Steel Institute) 1018 mit niedrigem Kohlenstoffgehalt. Stahl mit niedrigem Kohlenstoffgehalt wird für die meisten elektromagnetischen Antriebe verwendet. Es weist eine hohe Durchlässigkeit auf und ist relativ kostengünstig [12].
Die Magnete erzeugen eine Haltekraft, die von der Position des Ankers im Verhältnis zum Gehäuse abhängt (geringer und hoher magnetischer Widerstand).
Für die Analyse wurde die Magnetfeldphysik ausgewählt. Um die nichtlinearen magnetischen Eigenschaften des Kohlenstoffstahls und die remanente Flussdichte der Magnete zu definieren, wurde das Ampèresche Gesetz auf die relevanten Bereiche angewendet. Die nichtlinearen magnetischen Eigenschaften werden eingeführt, um die magnetische Sättigung (der Zustand, in dem die Magnetisierung eines
Materials einen Punkt erreicht, an dem sie aufgrund des externen angewendeten Magnetfeldes H nicht weiter zunehmen kann) [2] [3].
Für die Berechnung der elektromagnetischen Kraft im Anker wurde die Methode des Maxwellschen Spannungstensors angewendet. Dieser Tensor ist mathematisch ein Integral entlang eines abgeschlossenen Weges (in 2D) oder einer abgeschlossenen Oberfläche „A“ (in 3D) um einen Bereich von Interesse. Eine der Einschränkungen dieser Methode besteht darin, dass zwischen einem magnetischen Material und einer magnetischen Materialschnittstelle (Pole) ein sehr kleiner Luftspalt (< 0,1 mm) aufrechterhalten werden muss. Andernfalls wird ein sehr niedriger Kraftwert berechnet, der nicht dem realen Wert entspricht [12] [5].
Dynamische Analyse
Zur Untersuchung des dynamischen Verhaltens des Antriebs wurden zwei Modelle simuliert, um die Öffnungs- und Schließleistung zu berücksichtigen [4] [7] [8]. Der Stromkreis, mit dem der Antrieb betrieben wird, wird unten dargestellt (Abbildung 2):

Beim Öffnen wird der Strom in der Spule abgeschaltet. Dann wird die induzierte Spannung (und damit der induzierte Strom) mit dem TVS unterdrückt. Beim Schließen wird eine Impulssequenz aus der Stromquelle des Antriebs (APS, Actuator Power Source) verwendet, um den Antrieb zu betreiben.
Die gelösten Gleichungen ((1) – (3)) lauten wie folgt:
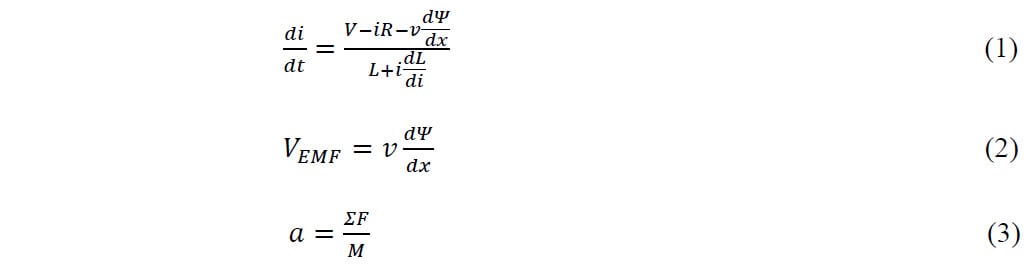
V: Spannung (V), i: Strom (A), R: Widerstand (Ω), L: Induktivität (H), VEMF: EMK-Gegenspannung (V), v: Geschwindigkeit (m/s), α: Beschleunigung (m/s2), t: Zeit (s)ΣF: Gesamtkraft (N), M: Masse (kg), Ψ: Flussverkettung (Wb-T). Die Flussverkettungen bestehen aus zwei Komponenten: Eine Komponenten ist von dem Magnetfeld abhängig, das die Dauermagneten (BPM) erzeugen, und die andere von dem durch die Spule (Bc) erzeugten Magnetfeld.
Die Wirbelströme wurden mit folgender Gleichung berechnet [1]:
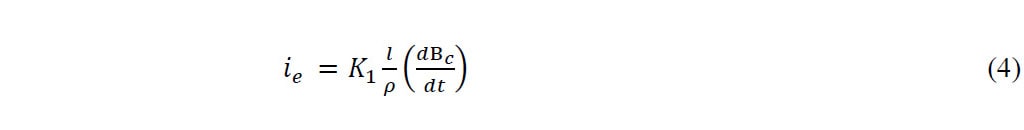
Wobei K1 ein geometrischer Faktor, l die Länge des Kolbens und ρ der spezifische Widerstand des Materials ist [1]. Vorausgesetzt, der Kolben ist ein Zylinder, lautet Gleichung 4 wie folgt:

Das Magnetfeld, das durch die Wirbelströme (Be) und die entsprechende Kraft (Fe) erzeugt wurde, wurde mit Gleichungen 6 und 7 berechnet.
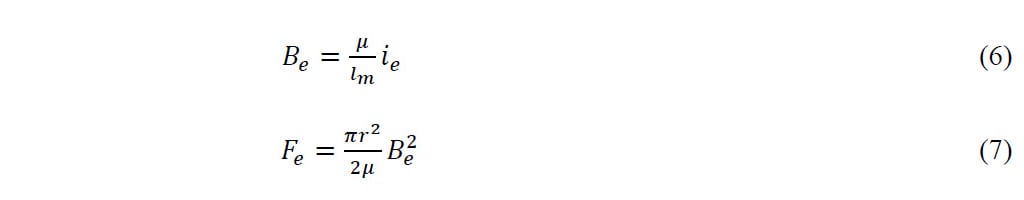
Wobei lm der magnetische Weg, r der Radius des Kolbens und μ die Dielektrizitätskonstante des Materials ist.
Simulationsergebnisse
Die Magnetfeldverteilung in verschiedenen Positionen wird in Abbildung 3 dargestellt.
In der Schließposition (Abbildung 3a) bildet der Anker zusammen mit dem Stahlgehäuse einen Weg mit geringem magnetischen Widerstand, während die große Lücke oben einen Weg mit hohem magnetischen Widerstand darstellt. Daher verlaufen die Magnetfeldlinien fast ausschließlich durch das Ende des Ankers, der Kontakt zum Gehäuse hat. Die Haltekraft, die von den Magneten in dieser
Position erzeugt wird, weist einen hohen Wert auf. Für einen ausfallsicheren Betrieb wird die Spule auch verwendet, um eine noch höhere Haltekraft zu erzeugen und den Anker in der Schließposition zu halten.
Für die Öffnung wird der Strom, der durch die Spule fließt, abgeschaltet, und der Anker bewegt sich. Während der Anker sich von der Schließposition in die Öffnungsposition bewegt, werden die Magnetfeldlinien in Richtung des Weges mit dem zuvor geringeren Widerstand verschoben (Abbildung 3b), da nun der Luftspalt in der Öffnungsposition immer kleiner wird bzw. der magnetische Widerstand abnimmt. Daher nimmt die Haltekraft unten ab, während die Anziehungskraft oben steigt.

Wenn der Anker die Öffnungsposition erreicht (Abbildung 3c), ist der Widerstandsweg umgekehrt, sodass sich die Magnetfeldlinien hauptsächlich oben konzentrieren. Die Magnetfeldkonzentrationen in der Schließ- und in der Öffnungsposition des Ankers sind also unterschiedlich. Daher weist die Haltekraft in der Öffnungsposition einen niedrigeren Wert auf als in der Schließposition. Die Ergebnisse der dynamischen Analyse werden in den Abbildungen 4 und 5 dargestellt:


Einige vorläufige experimentelle Ergebnisse (Abbildungen 6 und 7) in leicht unterschiedlichen Antriebsmodellen (Designs vor den endgültigen Anpassungen) belegen das Konzept des vorgeschlagenen Designs und Steuerungskreises.

Das Profil der dynamischen Eigenschaften, die bei der Prüfung beobachtet wurden, stimmt mit den Simulationsergebnissen überein. Die Geschwindigkeitswerte und die Dauer des Schließ- und Öffnungsvorgangs sind in Tests und Simulationen ähnlich (Fehlerquote unter 10 %).
ERÖRTERUNG UND KERNASPEKTE
Das optimierte Modell des Antriebs soll die Wirkung der elektromagnetischen Bremsung durch Induktion minimieren oder gar eliminieren. Zur Unterdrückung dieses Effekts beim Öffnen wird ein neuartiger Steuerungskreis verwendet, während beim Schließen eine Impulsfolge induziert wird, um die Leistung des Antriebs zu steuern.
Das innovative Antriebsdesign und der neuartige Steuerungskreis, der die Effizienz und Leistung des Systems verbessert (geringe Verlustleistung), tragen wesentlich zur Weiterentwicklung der neuen Generation der Dachaufbauten von Zügen von TE bei. Der Antrieb ist für zuverlässigen Betrieb ausgelegt und entspricht in Bezug auf sein flaches Profil und seine leichte Bauweise
den Marktanforderungen (Verbesserung der aerodynamischen Leistung). Zudem ist der Stromverbrauch minimal.
Basierend auf dem Vergleich zwischen Test- und Simulationsergebnissen wird der Schluss gezogen, dass die vorgeschlagene Berechnungsmethode die transienten Eigenschaften eines elektromagnetischen Antriebs genau analysieren kann. Es sei darauf hingewiesen, dass in diesem Bericht der Effekt des Wirbelstroms berücksichtigt wird. Aufgrund seiner Komplexität
ist dies in den meisten vorhandenen Berichten nicht der Fall. Daher liegt die Bedeutung dieser Methode darin, dass sie vor dem Prototyping eingesetzt werden kann, um Zeit, Kosten und Ressourcen während der Konstruktion und Fertigung deutlich zu reduzieren.
ANERKENNUNGEN
Wir möchten Graham Mcdonald, Robert Phillpotts und Thomas Moore für die Unterstützung und die kompetente Beratung während des gesamten Projekts danken. Sie stellten die mechanischen Modelle und die Elektronikkonfigurationen nach den Empfehlungen aus der Analyse und den Daten für die mechanischen Kräfte bereit.
VERWEISE
[1] Mandache, L.; D. Topan; K. Al Haddad. „Modeling of Non-Linear Ferromagnetic Cores“. Revue Roumaine de Sciences Techniques. Serie Electrotechnique et Energetique. Band 53, Ausgabe 4. 2008.
[2] K. Srairi und M. Feliachi, „Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators“, IEEE Transactions on Magnetics, Band 34, Nr. 5, Seite 3608–3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov und D. Dimitrov, „Dynamic characteristics of a permanent magnet electromagnetic valve actuator“ in 12th International Conference on Optimization of Electrical and Electronic Equipment, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov und K. Hinov, „Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator“, Elec. Energ., Band 23, Nr. 1, Seite 37–43, 2010.
[5] I. Yatchev und E. Ritchie, „Simulation of Dynamics of a Permanget Linear Actuator“, International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, Band 4, Nr. 6, S. 726–730, 2010.
[6] S.-M. Wang, T. Miyano und M. Hubbard, „Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator“, IEEE Transactions on Magnetics, Band 29, Nr. 2, S. 1741–1746, 1993.
[7] A. Radulian und N. Mocioi, „Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors“. International Conference and Exposition on Electrical and Power Engineering, Iasi, Rumänien, 2014.
[8] N. Paudel, „Part 1: How to Model a Linear Electromagnetic Plunger“, 7. Juni 2016. [Online]. Verfügbar unter https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, „Part 2: Model a Linear Electromagnetic Plunger with a Blocker“, 14. Juni 2016. [Online]. Verfügbar unter https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer und B. Ulrych, „Electromechanical Actuators Dynamics“, J. of Electrical Engineering, Band 60, Nr. 5, S. 255, 2009.
[11] H. Musaab, „Using Look-up Tables to Model an Electromagnetic Suspansion System“, American Journal of Applied Sciences, Band 9, Nr. 8, S. 1199–1202, 2012.
[12] O. Vogel und J. Ulm, „Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics“, COMSOL-Konferenz, Stuttgart, 2011.
