Análise do atuador eletromagnético linear utilizando FEA
RESUMO
Neste artigo, analisamos as características dinâmicas de um atuador eletromagnético, utilizado para disjuntores a vácuo. Os fenômenos magnéticos, elétricos e mecânicos são simultaneamente analisados para obter o comportamento dinâmico do atuador. Os parâmetros magnéticos são computados usando análise de elementos finitos (FEA) e, em seguida, importados para um software de análise dinâmica, onde as equações elétricas e mecânicas são calculadas. Os resultados da análise, juntamente com alguns dados experimentais, são apresentados. Essa técnica pode ser usada para analisar de forma muito precisa o comportamento eletromagnético dinâmico de sensores, relés, interruptores e outros sistemas atuadores.
DECLARAÇÃO DO PROBLEMA
O atuador eletromagnético é amplamente utilizado em disjuntores. Seu papel é realizar o movimento dos contatos móveis da garrafa de vácuo com certas velocidades e trajetórias precisas.
Neste relatório, é proposto e analisado um novo modelo de atuador linear, que será usado na nova geração dos sistemas de linha de teto de material rodante em trilhos da TE. Um fator que afeta significativamente o funcionamento do atuador é a força de arrasto magnético. Essa força pode ser decorrente de:
- Campo magnético estático: à medida que a armadura se move, ele experimenta a atração magnética (devido ao movimento relativo com os ímãs, dependendo da posição).
- Corrente de bobina residual: quando a tensão de retenção é desconectada da bobina, leva tempo para que a corrente da bobina decaia a zero. Enquanto estiver presente, ela produz atração magnética para a posição de fechamento. O decaimento rápido pode ser obtido por:
o Aumento da tensão de TVS (supressor de tensão transitória)
o Indutância decrescente da bobina
- Correntes de fuga induzidas [1]
- Correntes de fuga induzidas por movimento: este efeito é responsável pela maior parte das perdas de energia (se houver um movimento relativo entre a armadura e os ímãs) e pode ser efetivamente reduzido ou até mesmo eliminado movendo os ímãs na armadura (e/ou usando ímãs com menor força de campo magnético) [1].
- Corrente EMF (força eletromotriz) de retorno: a armadura móvel causa tensão EMF de retorno — que, por sua vez, causa a corrente EMF de retorno que age contra o movimento.
Pesquisas anteriores não explicam o efeito das correntes de fuga no movimento da armadura do atuador; mas, por ser fundamental para o desempenho do atuador, todos os efeitos acima mencionados foram levados em consideração, calculados e incluídos no modelo. Assim, nosso modelo prevê com alta precisão o comportamento real do atuador antes da prototipagem e pode ser usado para análise de sensibilidade para reduzir o tempo de projeto e custo, proporcionando uma solução técnica e econômica ideal. A descrição mais detalhada dos métodos e resultados seguirá nas próximas seções.
MÉTODOS E RESULTADOS
Análise estática
A Fig. 1 mostra a estrutura proposta do atuador eletromagnético:
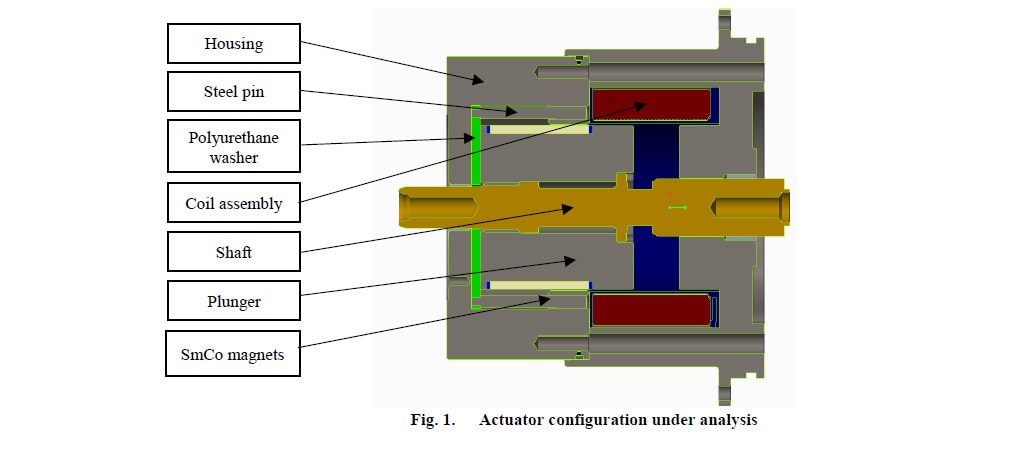
Em comparação com um atuador típico (que geralmente consiste em uma bobina de abertura e outra de fechamento), este tipo de atuador consiste em um invólucro (ou estrutura), pino de aço, conjunto da bobina (carretel e enrolamentos), armadura (êmbolo), eixo, arruela de poliuretano e ímãs permanentes de SmCo (samário-cobalto) (PM).
As curvas da bobina criam um campo eletromagnético quando a corrente é aplicada em seus terminais. O objetivo da bobina é conduzir a armadura para a posição fechada e ajudar a segurá-la lá. Este atuador deve entrar em modo failsafe (aberto) em caso de perda de energia na bobina. O processo de abertura começa quando a corrente na bobina é cortada, e obtido apenas por
meios mecânicos (molas etc.). Assim, a dissipação de energia (crítica para trens modernos) neste tipo de atuador é significativamente menor que a dissipação em um atuador típico, enquanto a segurança é prioridade.
O estator concentra o campo magnético. Ele envolve o exterior da bobina e é feito de aço de baixo carbono AISI (American Iron and Steel Institute) 1018. O aço de baixo carbono é usado para a maioria dos atuadores eletromagnéticos. Ele tem uma alta permeabilidade e um custo relativo baixo [12].
Os ímãs estão produzindo uma força de retenção que depende da posição da armadura em relação ao invólucro (baixa e alta relutância magnética).
Para a análise, foi selecionada a física dos campos magnéticos. Para definir as propriedades magnéticas não lineares do aço carbono e a densidade de fluxo remanente dos ímãs, a Lei de Ampère é aplicada aos domínios relevantes. As propriedades magnéticas não lineares são introduzidas para explicar a saturação magnética (o estado quando a magnetização de um
material atinge um ponto onde não pode aumentar ainda mais devido ao aumento do campo magnético externo aplicado H) [2] [3].
Para o cálculo da força eletromagnética na armadura, foi aplicado o método do tensor de tensões de Maxwell foi aplicado. Esse tensor é matematicamente uma integral ao longo de um caminho fechado (em 2D) ou uma área de superfície fechada "A" (em 3D) em torno de um domínio de interesse. Uma das limitações desse método é que, quando há uma interface de material magnético para material magnético (atuando como polos), uma lacuna de ar muito pequena (<0,1 mm) deve ser mantida entre eles; caso contrário, um valor muito baixo da força é calculado, o que não corresponde ao seu valor real [12] [5].
Análise dinâmica
Para estudar o comportamento dinâmico do atuador, foram simulados dois modelos para explicar seu desempenho de abertura e fechamento [4] [7] [8]. O circuito elétrico usado para acionar o atuador é mostrado abaixo (Fig. 2):
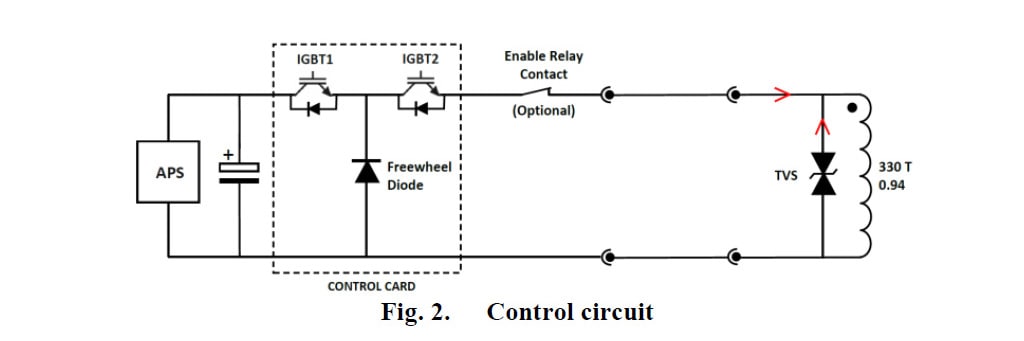
Durante a abertura, a corrente na bobina é cortada e a TVS é usada para suprimir a tensão induzida (e, consequentemente, a corrente induzida). Durante o fechamento, uma sequência de pulso do APS (fonte de energia do atuador) é usada para acionar o atuador.
As equações resolvidas ((1) — (3)) são as seguintes:
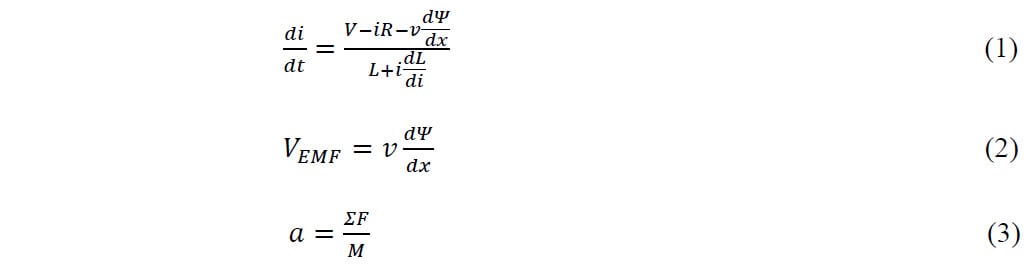
V: tensão (V), i: corrente (A), R: resistência (Ω), L: indutância (H), VEMF: tensão EMF de retorno (V), v: velocidade (m/s), α: aceleração (m/s2), t: tempo (s), ΣF: força total (N), M: massa (kg), Φ: ligação de fluxo (Wb-T). As ligações de fluxo têm dois componentes: um dependente do campo magnético produzido pelo PM (BPM) e outro componente devido ao campo magnético produzido pela bobina (Bc).
As correntes de fuga foram calculadas usando a seguinte equação [1]:
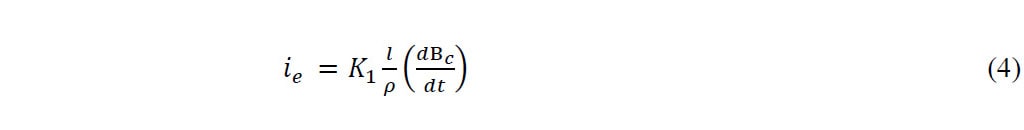
Onde K1 é um fator geométrico, l é o comprimento do êmbolo e ρ é a resistividade material [1]. Assumindo o êmbolo como uma equação de cilindro, 4 se torna:

O campo magnético produzido pelas correntes de fuga (Be) e a força correspondente (Fe) foram calculados utilizando-se equações 6 e 7.
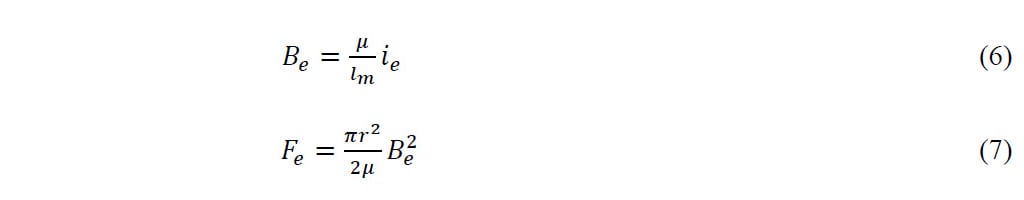
Onde lm é o caminho magnético, r é o raio do êmbolo e μ a permissividade do material.
Resultados da simulação
A distribuição do campo magnético em diferentes posições é mostrada na Fig. 3.
Na posição fechada (Fig. 3a), a armadura, junto com a carcaça de aço, forma um caminho de baixa relutância magnética, enquanto a grande lacuna no topo representa um caminho de alta resistência magnética. Portanto, as linhas de campo magnético funcionam quase exclusivamente até o final da armadura estar em contato com o invólucro. A força de retenção produzida pelos ímãs nesta
posição é de alto valor. Para conseguir uma operação à prova de falhas, a bobina também é usada para produzir uma força de retenção ainda maior para manter a armadura na posição fechada.
Para abrir, a corrente que flui através da bobina é cortada e a armadura começa a se mover. À medida que a armadura se move da posição fechada à posição aberta, as linhas de campo magnético são empurradas para o caminho anteriormente inferior (Fig. 3b), pois agora a lacuna de ar na posição aberta está ficando cada vez menor (a relutância magnética está ficando menor). Assim, a força de retenção na parte inferior diminui, enquanto a atração no topo aumenta.
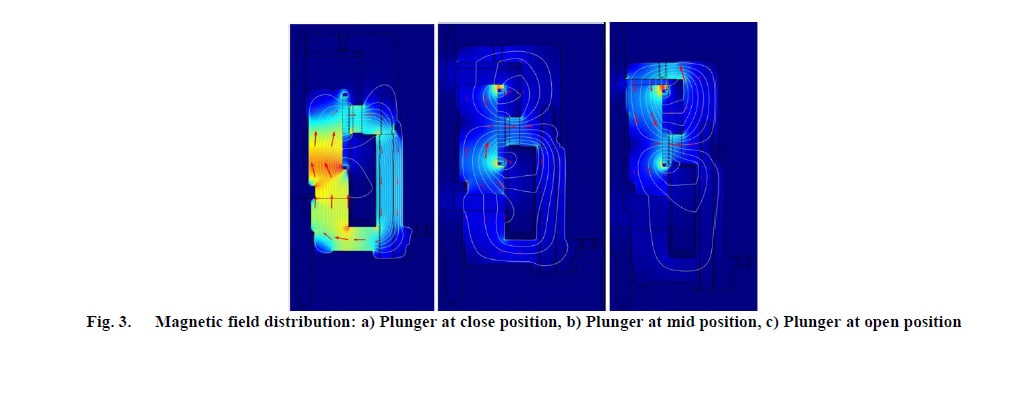
Quando a armadura atinge a posição aberta (Fig. 3c), o caminho de relutância é oposto ao mencionado anteriormente, de modo que as linhas de campo magnético estão concentradas principalmente no topo. Como mostrado, a concentração do campo magnético não é semelhante quando a armadura está próxima e em posição aberta. Portanto, a força de retenção na posição aberta terá um valor menor do que o da posição próxima. Os resultados da análise dinâmica são mostrados nas Fig. 4 e 5:
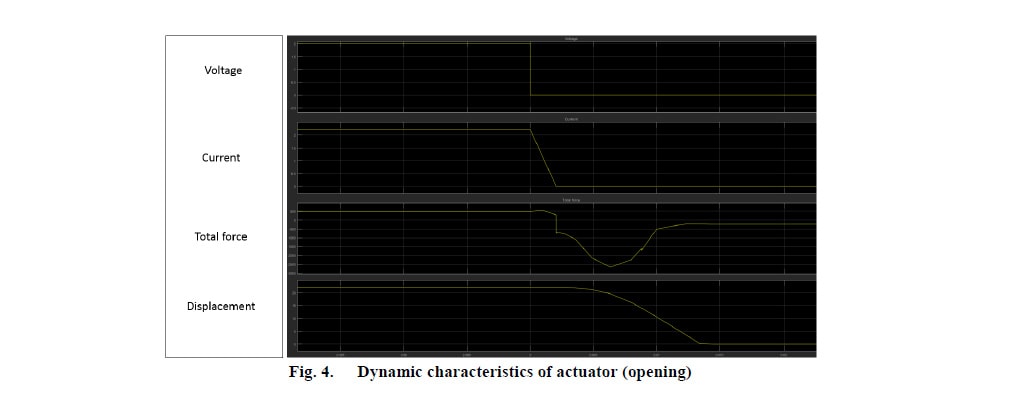
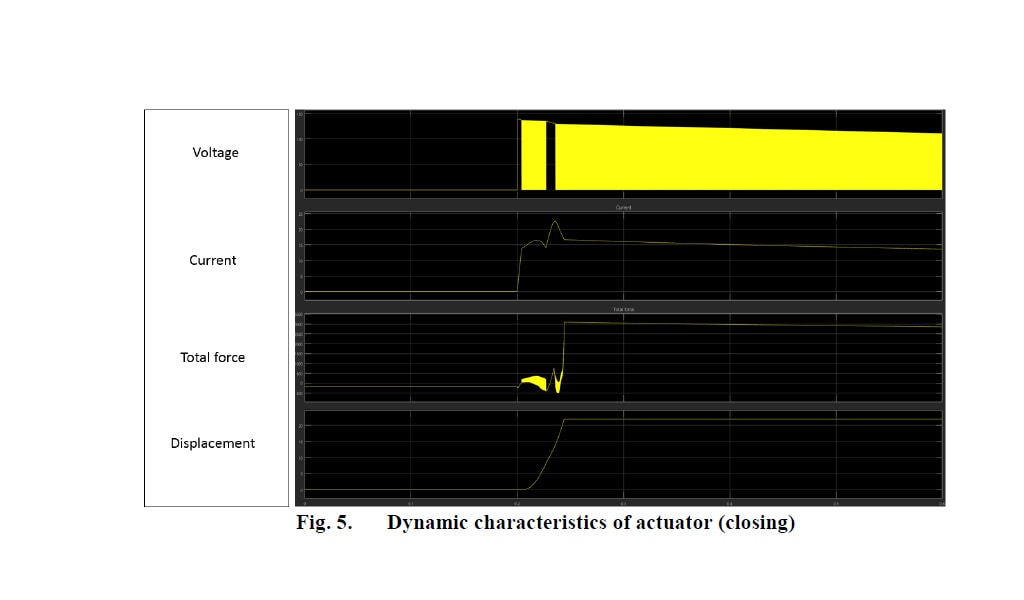
Alguns resultados experimentais preliminares (Fig. 6 e 7) em modelos de atuadores ligeiramente diferentes (desenhos antes dos ajustes finais) comprovam o conceito do design e do circuito de controle proposto.
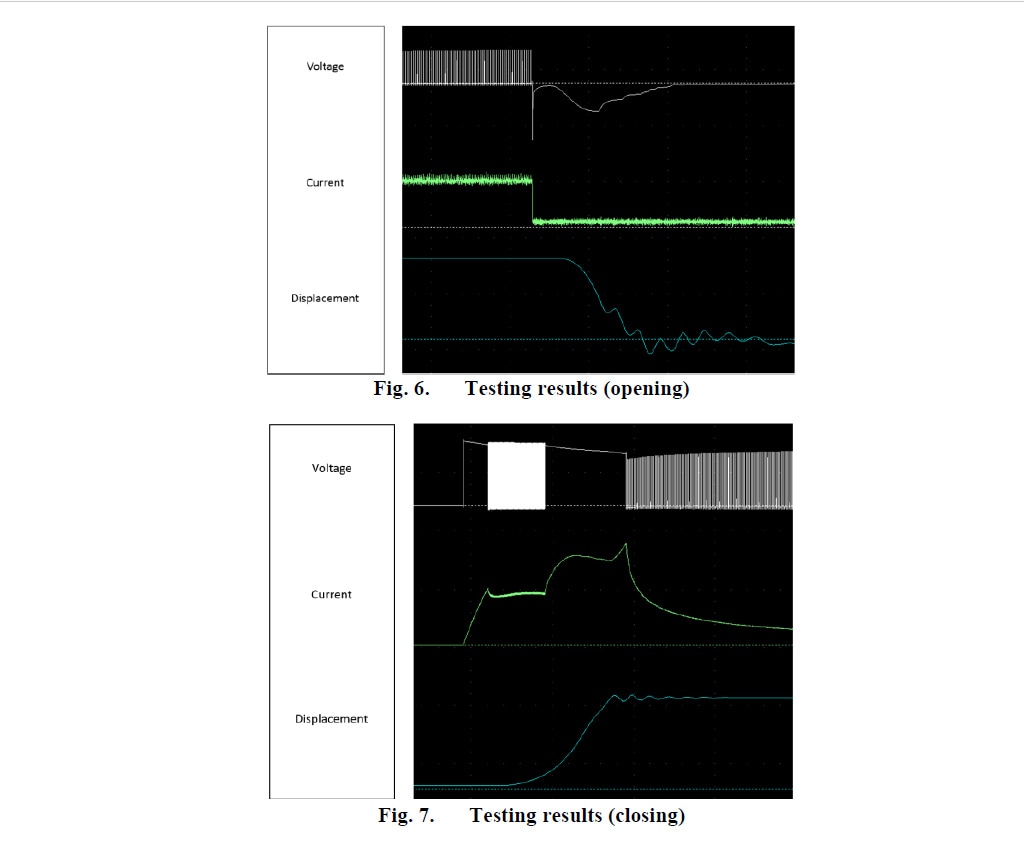
O perfil das características dinâmicas observadas durante os testes vem de acordo com os resultados da simulação. Os valores da velocidade e da duração da operação de fechamento e abertura são semelhantes em testes e simulações (erro de menos de 10%).
DISCUSSÃO E PONTOS-CHAVE
O modelo otimizado do atuador é proposto para minimizar ou mesmo eliminar o efeito da frenagem eletromagnética devido à indução. Um novo circuito de controle é usado para suprimir esse efeito durante a abertura, enquanto, durante o fechamento, uma sequência pulsante é introduzida para controlar o desempenho do atuador.
O design inovador do atuador e o circuito de controle que melhora a eficiência e o desempenho do sistema (baixa dissipação de energia) contribuem significativamente para o desenvolvimento contínuo da nova geração de sistemas de linha de teto de trens da TE. O atuador foi projetado para alcançar uma operação confiável e está em conformidade com os requisitos de perfil baixo e leve do mercado
(melhoria do desempenho aerodinâmico) e consumo mínimo de energia.
Com base na comparação entre os resultados de testes e da simulação, conclui-se que o método de cálculo proposto pode analisar com precisão as características transitórias de um atuador eletromagnético, ao mesmo tempo em que vale ressaltar que a contribuição atual da corrente de fuga é considerada neste relatório, o que não é o fato na maioria dos artigos existentes devido à sua
forma complicada. Portanto, a importância deste método é que ele possa ser usado antes da prototipagem para reduzir significativamente o tempo, o custo e os recursos durante o projeto e a fabricação.
AGRADECIMENTOS
Queremos agradecer a Graham McDonald, Robert Phillpotts e Thomas Moore por todo o apoio e conselhos de especialistas ao longo deste projeto. Eles forneceram os modelos mecânicos e as configurações eletrônicas seguindo as recomendações da análise e os dados para as forças mecânicas.
REFERÊNCIAS
[1] Mandache, L.; D. Topan; K. Al Haddad. “Modeling of Non-Linear Ferromagnetic Cores”. Revue Roumaine de Sciences Techniques. Serie Electrotechnique et Energetique. Vol. 53, Issue 4. 2008.
[2] K. Srairi and M. Feliachi, “Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators,” IEEE Transactions on Magnetics, vol. 34, no. 5, pp. 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov and D. Dimitrov, “Dynamic characteristics of a permanent magnet electromagnetic valve actuator,” in 12th International Conference on Optimization of Electrical and Electronic Equipment, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov and K. Hinov, “Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator,” Elec. Energ., vol. 23, no. 1, pp. 37-43, 2010.
[5] I. Yatchev and E. Ritchie, “Simulation of Dynamics of a Permanent Manget Linear Actuator,” Internation Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, no. 6, pp. 726-730, 2010.
[6] S.-M. Wang, T. Miyano and M. Hubbard, “Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator” IEEE Transactions on Magnetics, vol. 29, no. 2, pp. 1741-1746, 1993.
[7] A. Radulian and N. Mocioi, “Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors”. International Conference and Exposition on Electrical and Power Engineering, Iasi, Romania, 2014.
[8] N. Paudel, “Part 1: How to Model a Linear Electromagnetic Plunger,” 7th June 2016. [Online]. Available: https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, “Part 2: Model a Linear Electromagnetic Plunger with a Blocker,” 14th June 2016. [Online]. Available: https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer and B. Ulrych, “Electromechanical Actuators Dynamics” J. of Electrical Engineering, vol. 60, no. 5, pp. 255, 2009.
[11] H. Musaab, “Using Look-up Tables to Model an Electromagnetic Suspansion System,” American Journal of Applied Sciences, vol. 9, no. 8, pp. 1199-1202, 2012.
[12] O. Vogel and J. Ulm, “Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics,” in Comsol Conference, Stuttgart, 2011.
Análise do atuador eletromagnético linear utilizando FEA
RESUMO
Neste artigo, analisamos as características dinâmicas de um atuador eletromagnético, utilizado para disjuntores a vácuo. Os fenômenos magnéticos, elétricos e mecânicos são simultaneamente analisados para obter o comportamento dinâmico do atuador. Os parâmetros magnéticos são computados usando análise de elementos finitos (FEA) e, em seguida, importados para um software de análise dinâmica, onde as equações elétricas e mecânicas são calculadas. Os resultados da análise, juntamente com alguns dados experimentais, são apresentados. Essa técnica pode ser usada para analisar de forma muito precisa o comportamento eletromagnético dinâmico de sensores, relés, interruptores e outros sistemas atuadores.
DECLARAÇÃO DO PROBLEMA
O atuador eletromagnético é amplamente utilizado em disjuntores. Seu papel é realizar o movimento dos contatos móveis da garrafa de vácuo com certas velocidades e trajetórias precisas.
Neste relatório, é proposto e analisado um novo modelo de atuador linear, que será usado na nova geração dos sistemas de linha de teto de material rodante em trilhos da TE. Um fator que afeta significativamente o funcionamento do atuador é a força de arrasto magnético. Essa força pode ser decorrente de:
- Campo magnético estático: à medida que a armadura se move, ele experimenta a atração magnética (devido ao movimento relativo com os ímãs, dependendo da posição).
- Corrente de bobina residual: quando a tensão de retenção é desconectada da bobina, leva tempo para que a corrente da bobina decaia a zero. Enquanto estiver presente, ela produz atração magnética para a posição de fechamento. O decaimento rápido pode ser obtido por:
o Aumento da tensão de TVS (supressor de tensão transitória)
o Indutância decrescente da bobina
- Correntes de fuga induzidas [1]
- Correntes de fuga induzidas por movimento: este efeito é responsável pela maior parte das perdas de energia (se houver um movimento relativo entre a armadura e os ímãs) e pode ser efetivamente reduzido ou até mesmo eliminado movendo os ímãs na armadura (e/ou usando ímãs com menor força de campo magnético) [1].
- Corrente EMF (força eletromotriz) de retorno: a armadura móvel causa tensão EMF de retorno — que, por sua vez, causa a corrente EMF de retorno que age contra o movimento.
Pesquisas anteriores não explicam o efeito das correntes de fuga no movimento da armadura do atuador; mas, por ser fundamental para o desempenho do atuador, todos os efeitos acima mencionados foram levados em consideração, calculados e incluídos no modelo. Assim, nosso modelo prevê com alta precisão o comportamento real do atuador antes da prototipagem e pode ser usado para análise de sensibilidade para reduzir o tempo de projeto e custo, proporcionando uma solução técnica e econômica ideal. A descrição mais detalhada dos métodos e resultados seguirá nas próximas seções.
MÉTODOS E RESULTADOS
Análise estática
A Fig. 1 mostra a estrutura proposta do atuador eletromagnético:

Em comparação com um atuador típico (que geralmente consiste em uma bobina de abertura e outra de fechamento), este tipo de atuador consiste em um invólucro (ou estrutura), pino de aço, conjunto da bobina (carretel e enrolamentos), armadura (êmbolo), eixo, arruela de poliuretano e ímãs permanentes de SmCo (samário-cobalto) (PM).
As curvas da bobina criam um campo eletromagnético quando a corrente é aplicada em seus terminais. O objetivo da bobina é conduzir a armadura para a posição fechada e ajudar a segurá-la lá. Este atuador deve entrar em modo failsafe (aberto) em caso de perda de energia na bobina. O processo de abertura começa quando a corrente na bobina é cortada, e obtido apenas por
meios mecânicos (molas etc.). Assim, a dissipação de energia (crítica para trens modernos) neste tipo de atuador é significativamente menor que a dissipação em um atuador típico, enquanto a segurança é prioridade.
O estator concentra o campo magnético. Ele envolve o exterior da bobina e é feito de aço de baixo carbono AISI (American Iron and Steel Institute) 1018. O aço de baixo carbono é usado para a maioria dos atuadores eletromagnéticos. Ele tem uma alta permeabilidade e um custo relativo baixo [12].
Os ímãs estão produzindo uma força de retenção que depende da posição da armadura em relação ao invólucro (baixa e alta relutância magnética).
Para a análise, foi selecionada a física dos campos magnéticos. Para definir as propriedades magnéticas não lineares do aço carbono e a densidade de fluxo remanente dos ímãs, a Lei de Ampère é aplicada aos domínios relevantes. As propriedades magnéticas não lineares são introduzidas para explicar a saturação magnética (o estado quando a magnetização de um
material atinge um ponto onde não pode aumentar ainda mais devido ao aumento do campo magnético externo aplicado H) [2] [3].
Para o cálculo da força eletromagnética na armadura, foi aplicado o método do tensor de tensões de Maxwell foi aplicado. Esse tensor é matematicamente uma integral ao longo de um caminho fechado (em 2D) ou uma área de superfície fechada "A" (em 3D) em torno de um domínio de interesse. Uma das limitações desse método é que, quando há uma interface de material magnético para material magnético (atuando como polos), uma lacuna de ar muito pequena (<0,1 mm) deve ser mantida entre eles; caso contrário, um valor muito baixo da força é calculado, o que não corresponde ao seu valor real [12] [5].
Análise dinâmica
Para estudar o comportamento dinâmico do atuador, foram simulados dois modelos para explicar seu desempenho de abertura e fechamento [4] [7] [8]. O circuito elétrico usado para acionar o atuador é mostrado abaixo (Fig. 2):

Durante a abertura, a corrente na bobina é cortada e a TVS é usada para suprimir a tensão induzida (e, consequentemente, a corrente induzida). Durante o fechamento, uma sequência de pulso do APS (fonte de energia do atuador) é usada para acionar o atuador.
As equações resolvidas ((1) — (3)) são as seguintes:
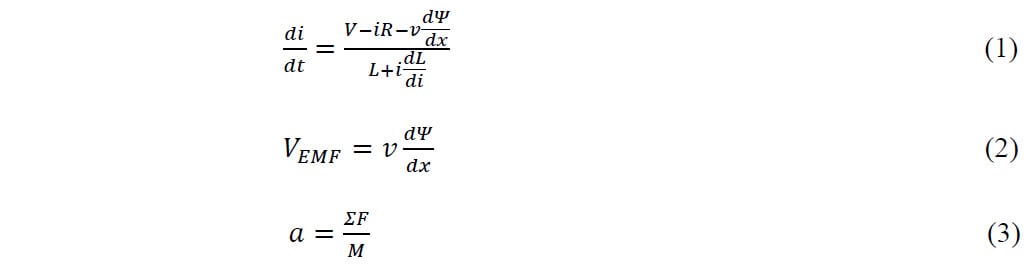
V: tensão (V), i: corrente (A), R: resistência (Ω), L: indutância (H), VEMF: tensão EMF de retorno (V), v: velocidade (m/s), α: aceleração (m/s2), t: tempo (s), ΣF: força total (N), M: massa (kg), Φ: ligação de fluxo (Wb-T). As ligações de fluxo têm dois componentes: um dependente do campo magnético produzido pelo PM (BPM) e outro componente devido ao campo magnético produzido pela bobina (Bc).
As correntes de fuga foram calculadas usando a seguinte equação [1]:
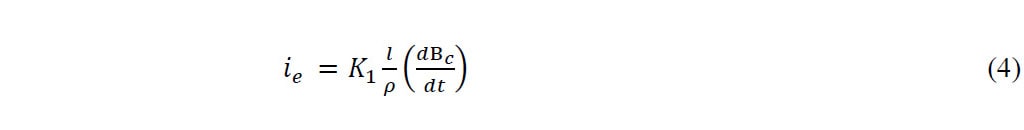
Onde K1 é um fator geométrico, l é o comprimento do êmbolo e ρ é a resistividade material [1]. Assumindo o êmbolo como uma equação de cilindro, 4 se torna:

O campo magnético produzido pelas correntes de fuga (Be) e a força correspondente (Fe) foram calculados utilizando-se equações 6 e 7.
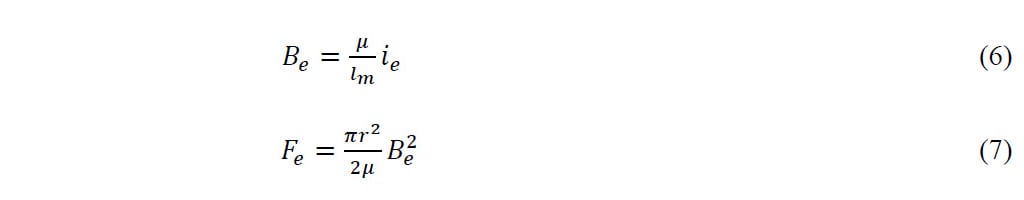
Onde lm é o caminho magnético, r é o raio do êmbolo e μ a permissividade do material.
Resultados da simulação
A distribuição do campo magnético em diferentes posições é mostrada na Fig. 3.
Na posição fechada (Fig. 3a), a armadura, junto com a carcaça de aço, forma um caminho de baixa relutância magnética, enquanto a grande lacuna no topo representa um caminho de alta resistência magnética. Portanto, as linhas de campo magnético funcionam quase exclusivamente até o final da armadura estar em contato com o invólucro. A força de retenção produzida pelos ímãs nesta
posição é de alto valor. Para conseguir uma operação à prova de falhas, a bobina também é usada para produzir uma força de retenção ainda maior para manter a armadura na posição fechada.
Para abrir, a corrente que flui através da bobina é cortada e a armadura começa a se mover. À medida que a armadura se move da posição fechada à posição aberta, as linhas de campo magnético são empurradas para o caminho anteriormente inferior (Fig. 3b), pois agora a lacuna de ar na posição aberta está ficando cada vez menor (a relutância magnética está ficando menor). Assim, a força de retenção na parte inferior diminui, enquanto a atração no topo aumenta.

Quando a armadura atinge a posição aberta (Fig. 3c), o caminho de relutância é oposto ao mencionado anteriormente, de modo que as linhas de campo magnético estão concentradas principalmente no topo. Como mostrado, a concentração do campo magnético não é semelhante quando a armadura está próxima e em posição aberta. Portanto, a força de retenção na posição aberta terá um valor menor do que o da posição próxima. Os resultados da análise dinâmica são mostrados nas Fig. 4 e 5:


Alguns resultados experimentais preliminares (Fig. 6 e 7) em modelos de atuadores ligeiramente diferentes (desenhos antes dos ajustes finais) comprovam o conceito do design e do circuito de controle proposto.

O perfil das características dinâmicas observadas durante os testes vem de acordo com os resultados da simulação. Os valores da velocidade e da duração da operação de fechamento e abertura são semelhantes em testes e simulações (erro de menos de 10%).
DISCUSSÃO E PONTOS-CHAVE
O modelo otimizado do atuador é proposto para minimizar ou mesmo eliminar o efeito da frenagem eletromagnética devido à indução. Um novo circuito de controle é usado para suprimir esse efeito durante a abertura, enquanto, durante o fechamento, uma sequência pulsante é introduzida para controlar o desempenho do atuador.
O design inovador do atuador e o circuito de controle que melhora a eficiência e o desempenho do sistema (baixa dissipação de energia) contribuem significativamente para o desenvolvimento contínuo da nova geração de sistemas de linha de teto de trens da TE. O atuador foi projetado para alcançar uma operação confiável e está em conformidade com os requisitos de perfil baixo e leve do mercado
(melhoria do desempenho aerodinâmico) e consumo mínimo de energia.
Com base na comparação entre os resultados de testes e da simulação, conclui-se que o método de cálculo proposto pode analisar com precisão as características transitórias de um atuador eletromagnético, ao mesmo tempo em que vale ressaltar que a contribuição atual da corrente de fuga é considerada neste relatório, o que não é o fato na maioria dos artigos existentes devido à sua
forma complicada. Portanto, a importância deste método é que ele possa ser usado antes da prototipagem para reduzir significativamente o tempo, o custo e os recursos durante o projeto e a fabricação.
AGRADECIMENTOS
Queremos agradecer a Graham McDonald, Robert Phillpotts e Thomas Moore por todo o apoio e conselhos de especialistas ao longo deste projeto. Eles forneceram os modelos mecânicos e as configurações eletrônicas seguindo as recomendações da análise e os dados para as forças mecânicas.
REFERÊNCIAS
[1] Mandache, L.; D. Topan; K. Al Haddad. “Modeling of Non-Linear Ferromagnetic Cores”. Revue Roumaine de Sciences Techniques. Serie Electrotechnique et Energetique. Vol. 53, Issue 4. 2008.
[2] K. Srairi and M. Feliachi, “Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators,” IEEE Transactions on Magnetics, vol. 34, no. 5, pp. 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov and D. Dimitrov, “Dynamic characteristics of a permanent magnet electromagnetic valve actuator,” in 12th International Conference on Optimization of Electrical and Electronic Equipment, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov and K. Hinov, “Simulation of the Dynamic Behaviour of a Permanent Magnet Linear Actuator,” Elec. Energ., vol. 23, no. 1, pp. 37-43, 2010.
[5] I. Yatchev and E. Ritchie, “Simulation of Dynamics of a Permanent Manget Linear Actuator,” Internation Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, no. 6, pp. 726-730, 2010.
[6] S.-M. Wang, T. Miyano and M. Hubbard, “Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator” IEEE Transactions on Magnetics, vol. 29, no. 2, pp. 1741-1746, 1993.
[7] A. Radulian and N. Mocioi, “Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors”. International Conference and Exposition on Electrical and Power Engineering, Iasi, Romania, 2014.
[8] N. Paudel, “Part 1: How to Model a Linear Electromagnetic Plunger,” 7th June 2016. [Online]. Available: https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, “Part 2: Model a Linear Electromagnetic Plunger with a Blocker,” 14th June 2016. [Online]. Available: https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer and B. Ulrych, “Electromechanical Actuators Dynamics” J. of Electrical Engineering, vol. 60, no. 5, pp. 255, 2009.
[11] H. Musaab, “Using Look-up Tables to Model an Electromagnetic Suspansion System,” American Journal of Applied Sciences, vol. 9, no. 8, pp. 1199-1202, 2012.
[12] O. Vogel and J. Ulm, “Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics,” in Comsol Conference, Stuttgart, 2011.
