Análisis de actuadores electromagnéticos lineales utilizando FEA
RESUMEN
En este artículo, analizamos las características dinámicas de un actuador electromagnético, utilizado para cortacircuitos de vacío. Se analizan los fenómenos magnéticos, eléctricos y mecánicos de manera simultánea para obtener el comportamiento dinámico del actuador. Los parámetros magnéticos se computan utilizando el análisis de elementos finitos (FEA) y luego se importan al software de análisis dinámico, donde se calculan las ecuaciones eléctricas y mecánicas. Se presentan los resultados del análisis junto con algunos datos experimentales. Esta técnica se puede utilizar para analizar de una manera muy precisa el comportamiento electromagnético dinámico de sensores, relés, interruptores y otros sistemas de actuadores.
PLANTEAMIENTO DEL PROBLEMA
El actuador electromagnético es ampliamente utilizado en cortacircuitos. Su función es lograr el movimiento de los contactos móviles del frasco de vacío con determinadas velocidades y trayectorias precisas.
En este informe, se propone y analiza un nuevo modelo de un actuador lineal, que se utilizará en la próxima generación de los sistemas de línea de techo de material rodante de TE. Un factor que afecta en gran medida el funcionamiento del actuador es la fuerza de arrastre magnética. Esta fuerza podría deberse a los siguientes factores:
- Campo magnético estático: a medida que la estructura se mueve, experimenta una tracción magnética (debido al movimiento relativo con los imanes dependiendo de su posición).
- Corriente residual en la bobina: cuando el voltaje de retención se desconecta de la bobina, toma tiempo para que la corriente de la bobina disminuya a cero. Mientras está presente, produce una tracción magnética hacia la posición de cierre. La rápida disminución de la corriente se puede lograr mediante:
o Aumento del voltaje del supresor de voltaje transitorio (TVS)
o Disminución de la inductancia de la bobina
- Corrientes de Foucault inducidas [1]
- Corrientes de Foucault inducidas por el movimiento: este efecto representa la mayor parte de las pérdidas de energía (si hay un movimiento relativo entre la estructura y los imanes) y puede reducirse o incluso eliminarse efectivamente moviendo los imanes en la estructura (o usando imanes con menor intensidad de campo magnético) [1].
- Corriente de fuerza electromotriz (EMF) inversa: la estructura en movimiento causa voltaje de EMF inversa que a su vez causa corriente de EMF inversa que actúa contra el movimiento.
En investigaciones anteriores, no se había tenido en cuenta el efecto de las corrientes de Foucault en el movimiento de la estructura del actuador, pero, como elemento fundamental para el rendimiento del actuador, todos los efectos mencionados anteriormente se han tenido en cuenta, calculado e incluido en el modelo. Por lo tanto, nuestro modelo predice con alta precisión el comportamiento real del actuador antes de la creación de prototipos y se puede utilizar para el análisis de sensibilidad a fin de reducir el tiempo de diseño y el costo. De esta manera, se logra una solución técnica y económica óptima. En las siguientes secciones se brindará una descripción más detallada de los métodos y resultados.
MÉTODOS Y RESULTADOS
Análisis estático
En la figura 1 se muestra la estructura propuesta del actuador electromagnético:
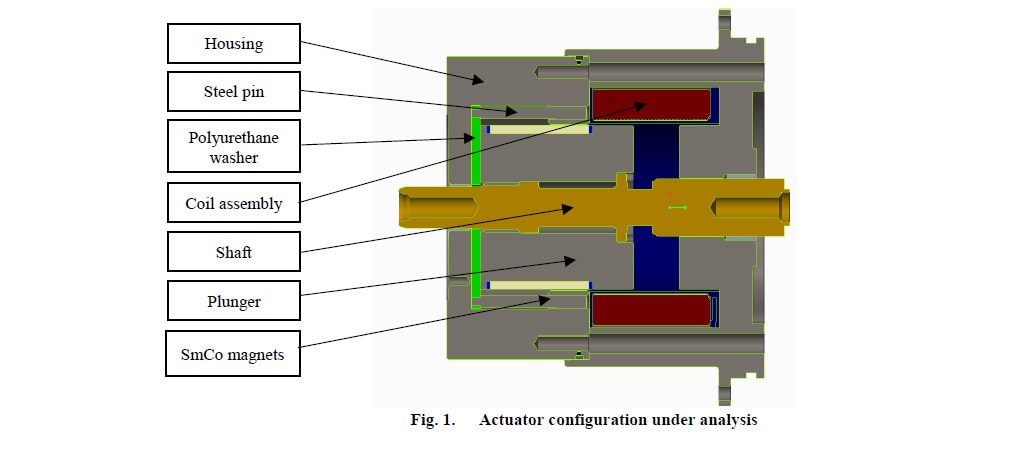
En comparación con un actuador típico (que generalmente consta de una bobina de apertura y cierre), este tipo de actuador consta de la carcasa (o marco), el conector de acero, el conjunto de la bobina (bobina y carrete), la estructura (émbolo), el eje, la arandela de poliuretano y los imanes permanentes (PM) de samario-cobalto (SmCo).
Los devanados de la bobina crean un campo electromagnético cuando la corriente se aplica a través de sus terminales. El propósito de la bobina es accionar la estructura en la posición cerrada y ayudar a mantenerla allí. Este actuador debería fallar, a prueba de errores (abierto) en caso de pérdida de potencia en la bobina. El proceso de apertura comienza cuando se corta la corriente en la bobina y se logra solo por
medios mecánicos (resortes, etc.). Por lo tanto, la disipación de potencia (crítica para los trenes modernos) en este tipo de actuador es significativamente menor que la disipación en un actuador típico, mientras que la seguridad es una prioridad.
El estator concentra el campo magnético. Rodea el exterior de la bobina y está hecho de acero con bajo contenido de carbono según la clasificación 1018 del Instituto Estadounidense del Hierro y el Acero (AISI). El acero con bajo contenido de carbono se utiliza para la mayoría de los actuadores electromagnéticos. Tiene una alta permeabilidad y un costo relativamente bajo [12].
Los imanes producen una fuerza de retención, que depende de la posición de la estructura en relación con la carcasa (reluctancia magnética baja y alta).
Para el análisis, se ha seleccionado la física de los campos magnéticos. Para definir las propiedades magnéticas no lineales del acero al carbono y la densidad de flujo remanente de los imanes, se ha aplicado la Ley de Ampère a los dominios relevantes. Las propiedades magnéticas no lineales se introducen para dar cuenta de la saturación magnética (el estado en que la magnetización de un
material alcanza un punto en el que no puede aumentar más debido al aumento del campo magnético externo aplicado H) [2] [3].
Para el cálculo de la fuerza electromagnética en la estructura, se ha aplicado el método del tensor de tensión de Maxwell. Este tensor es matemáticamente una integral a lo largo de una trayectoria cerrada (en 2D) o un área de superficie cerrada "A" (en 3D) en torno a un dominio de interés. Una de las limitaciones de este método es que, cuando se aplica un material magnético a la interfaz de material magnético (que actúa como polos), se debe mantener un espacio de aire muy pequeño (<0,1 mm) entre ellos; de lo contrario, se calcula un valor muy bajo de la fuerza, que no corresponde a su valor real [12] [5].
Análisis dinámico
Para estudiar el comportamiento dinámico del actuador se han simulado dos modelos para dar cuenta de su rendimiento de apertura y cierre [4] [7] [8]. El circuito eléctrico utilizado para accionar el actuador se muestra a continuación (figura 2):
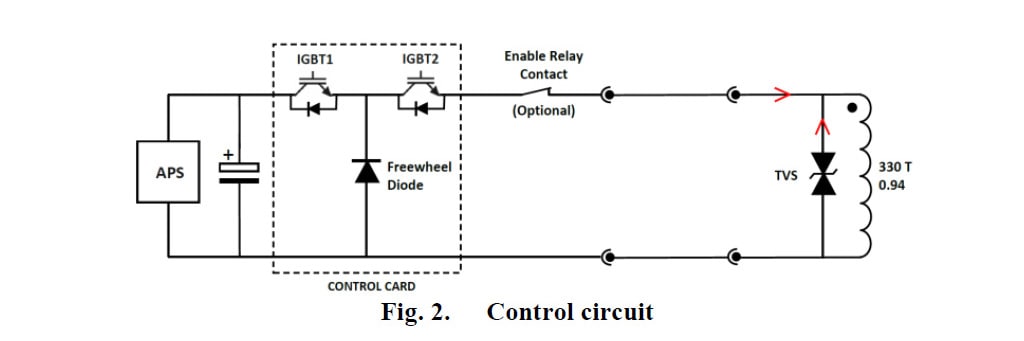
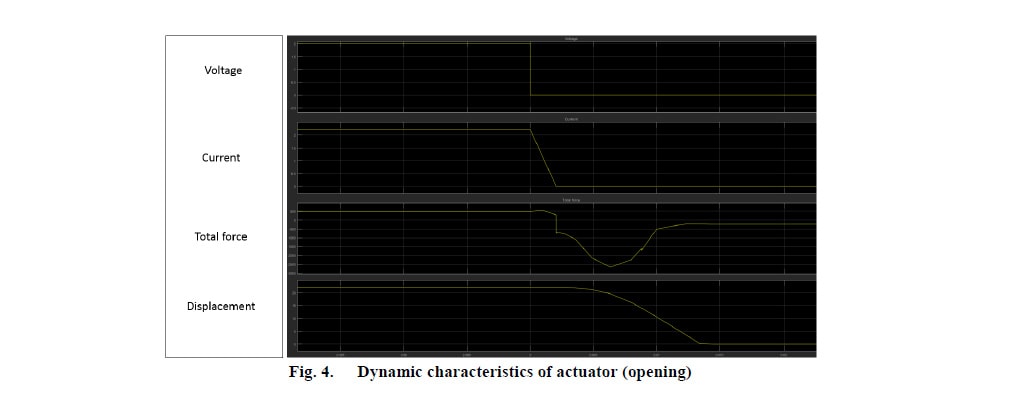
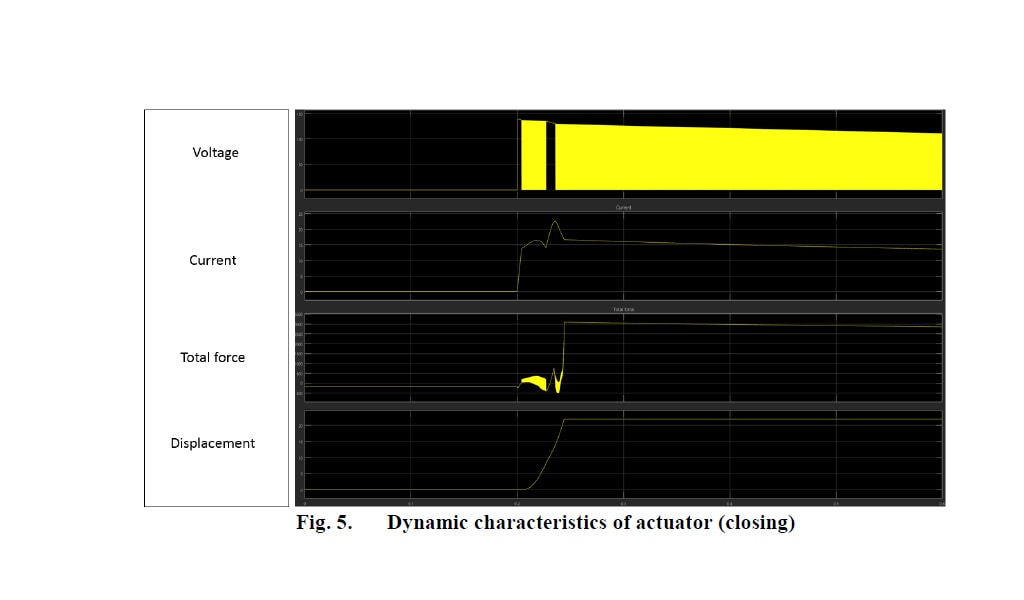
Durante la apertura, la corriente en la bobina se corta y se utiliza el TVS para suprimir el voltaje inducido (y en consecuencia la corriente inducida). Durante el cierre, se utiliza una secuencia de pulsos de la fuente de alimentación del actuador (APS) para accionar el actuador.
Las ecuaciones resueltas ((1) – (3)) son las siguientes:
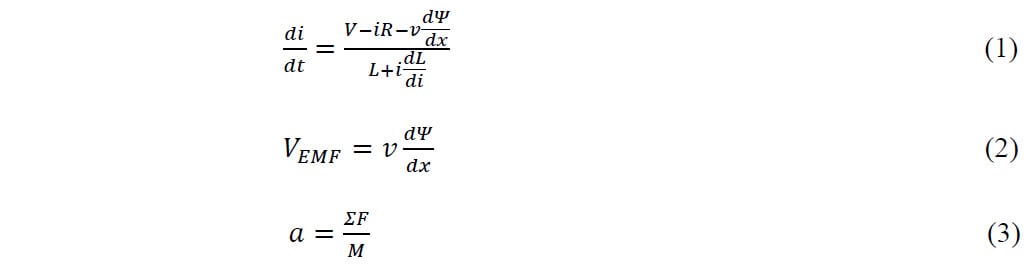
V: voltaje (V), i: corriente (A), R: resistencia (Ω), L: inductancia (H), VEMF: voltaje de EMF inversa (V), v: velocidad (m/s), α: aceleración (m/s2), t: tiempo (s) ΣF: fuerza total (N), M: masa (kg), Ψ: enlace de flujo (Wb-T). Los enlaces de flujo tienen dos componentes, uno de los cuales depende del campo magnético producido por el imán permanente sin escobillas (BPM) y otro componente debido al campo magnético producido por la bobina (Bc).
Las corrientes de Foucault se calcularon utilizando la siguiente ecuación [1]:
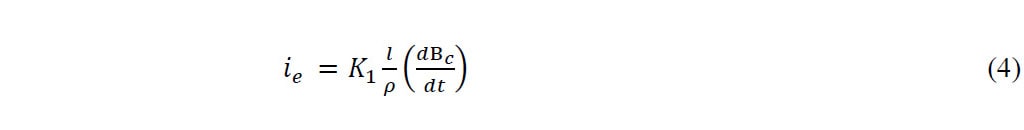
Donde K1 es un factor geométrico, l es la longitud del émbolo y ρ es la resistividad del material [1]. Suponiendo el émbolo como un cilindro, la ecuación 4 se convierte en lo siguiente:

El campo magnético producido por las corrientes de Foucault (Be) y la fuerza correspondiente (Fe) se calcularon utilizando las ecuaciones 6 y 7.
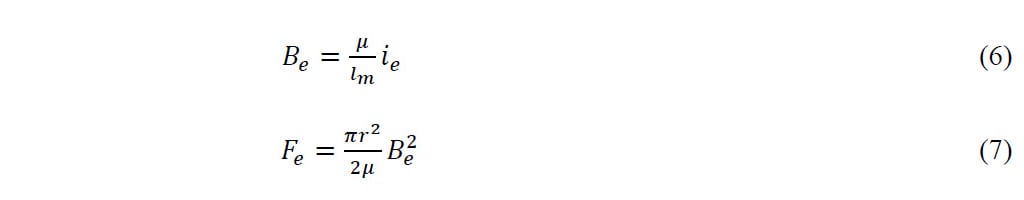
Donde lm es la trayectoria magnética, r es el radio del émbolo y μ la permitividad del material.
Resultados de la simulación
La distribución del campo magnético en diferentes posiciones se muestra en la figura 3.
En la posición cerrada (figura 3a), la estructura junto con la carcasa de acero forma una trayectoria de baja reluctancia magnética, mientras que el gran espacio en la parte superior representa una trayectoria de alta resistencia magnética. Por lo tanto, las líneas del campo magnético atraviesan casi exclusivamente el extremo de la estructura que está en contacto con la carcasa. La fuerza de retención producida por los imanes en esta
posición es de alto valor. Para lograr una operación a prueba de fallas, también se utiliza la bobina para producir una fuerza de retención aún mayor y mantener la estructura en la posición cerrada.
Para la apertura, la corriente que fluye a través de la bobina se corta y la estructura comienza a moverse. A medida que la estructura se mueve desde la posición cerrada a la abierta, las líneas del campo magnético se empujan hacia la trayectoria previamente inferior (figura 3b), ya que ahora el espacio de aire en la posición abierta es cada vez más pequeño (la reluctancia magnética es cada vez menor). Por lo tanto, la fuerza de retención en la parte inferior disminuye, mientras que la atracción en la parte superior aumenta.
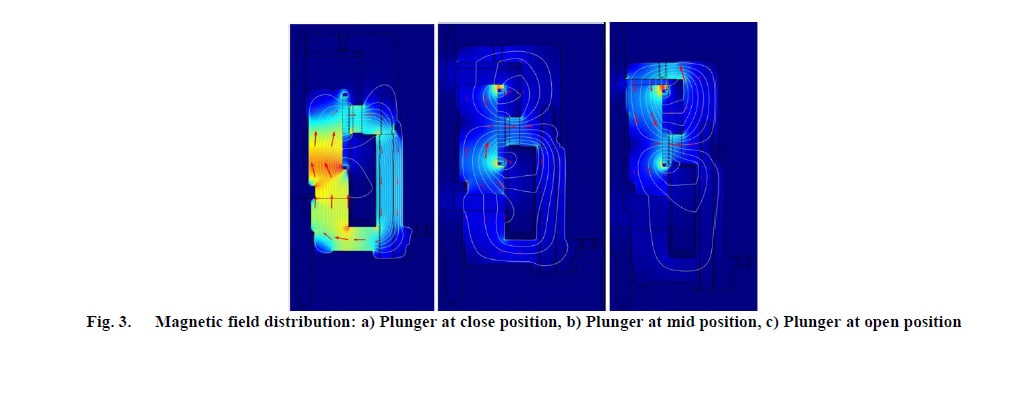
Cuando la estructura alcanza la posición abierta (figura 3c), la trayectoria de reluctancia es opuesta a la mencionada anteriormente, por lo que las líneas del campo magnético se concentran principalmente en la parte superior. Como se muestra, la concentración del campo magnético no es similar cuando la estructura está en posición cerrada y abierta. Por lo tanto, la fuerza de retención en la posición abierta tendrá un valor más bajo que la que está en la posición cerrada. Los resultados del análisis dinámico se muestran en las figuras 4 y 5:
Algunos resultados experimentales preliminares (figuras 6 y 7) en modelos de actuadores ligeramente diferentes (diseños anteriores a los ajustes finales) demuestran el concepto del diseño propuesto y el circuito de control.
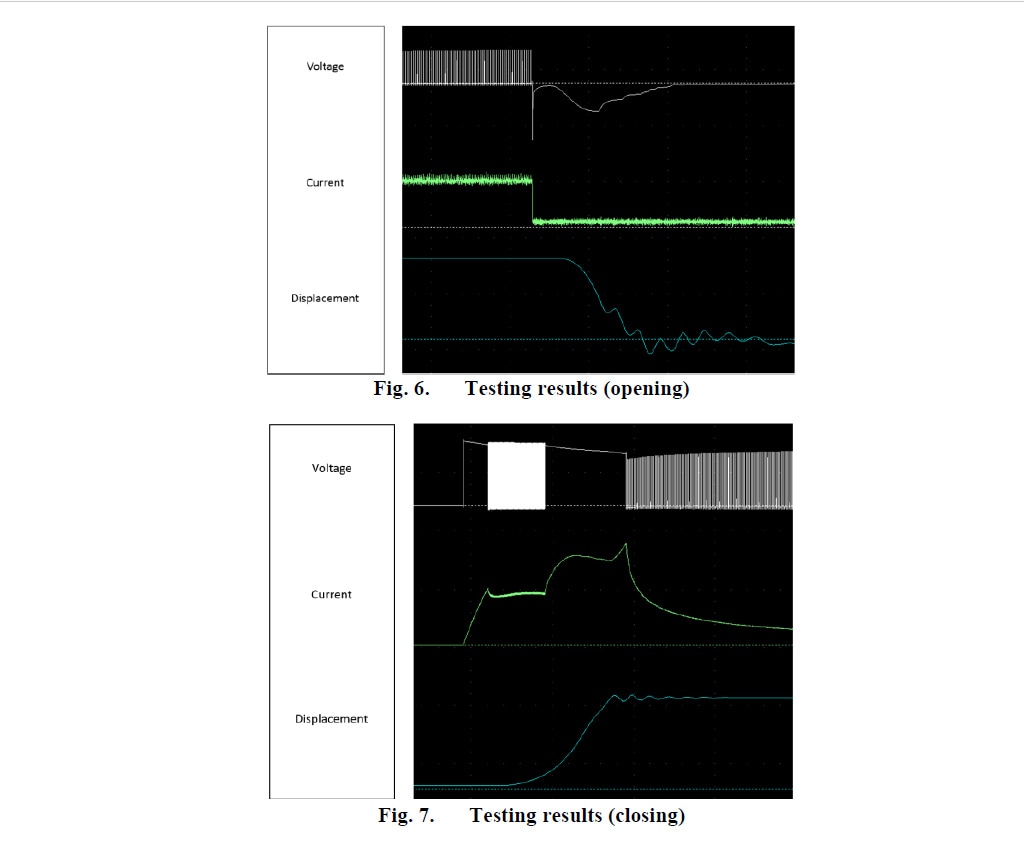
El perfil de las características dinámicas observadas durante las pruebas se condice con los resultados de la simulación. Los valores de la velocidad y la duración de la operación de cierre y apertura son similares en pruebas y simulaciones (menos del 10 % de error).
ANÁLISIS Y PUNTOS CLAVE
Se propone el modelo optimizado del actuador para minimizar o incluso eliminar el efecto del frenado electromagnético debido a la inducción. Se utiliza un nuevo circuito de control para suprimir este efecto durante la apertura, mientras que, durante el cierre, se introduce una secuencia pulsante para controlar el rendimiento del actuador.
El innovador diseño del actuador y el circuito de control que mejora la eficiencia y el rendimiento del sistema (baja disipación de potencia) contribuyen significativamente al desarrollo continuo de la próxima generación de sistemas de línea de techo para trenes de TE. El diseño del actuador permite lograr un funcionamiento fiable y se ajusta a los requisitos de perfil bajo y de ligereza del mercado
(mejora del rendimiento aerodinámico) y consume un nivel mínimo de energía.
Sobre la base de la comparación entre los resultados de las pruebas y la simulación, se llega a la conclusión de que el método de cálculo propuesto permite analizar con precisión las características transitorias de un actuador electromagnético. Sin embargo, cabe mencionar que, en este informe, se tiene en cuenta la contribución de la corriente de Foucault, lo que no sucede en la mayoría de los documentos existentes debido a su
forma complicada. Por lo tanto, la importancia de este método es que se puede utilizar antes de la creación de prototipos para reducir significativamente el tiempo, el costo y los recursos durante el diseño y la fabricación.
AGRADECIMIENTOS
Queremos agradecer a Graham Mcdonald, Robert Phillpotts y Thomas Moore por todo el apoyo y el asesoramiento experto que brindaron a lo largo de este proyecto. Proporcionaron los modelos mecánicos y las configuraciones electrónicas siguiendo las recomendaciones del análisis y los datos para las fuerzas mecánicas.
REFERENCIAS
[1] Mandache, L.; D. Topan; K. Al Haddad. “Modeling of Non-Linear Ferromagnetic Cores” (Modelado de núcleos ferromagnéticos no lineales). Revue Roumaine de Sciences Techniques. Serie Electrotechnique et Energetique. Vol. 53, número 4. 2008.
[2] K. Srairi y M. Feliachi, "Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators" (Modelos de acoplamiento numérico para analizar el comportamiento dinámico de los actuadores electromagnéticos), IEEE Transactions on Magnetics, vol. 34, núm. 5, pp. 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov y D. Dimitrov, "Dynamic characteristics of a permanent magnet electromagnetic valve actuator" (Características dinámicas de un actuador de válvula electromagnética de imán permanente), en la 12.ª Conferencia Internacional sobre Optimización de Equipos Eléctricos y Electrónicos, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov y K. Hinov, "Simulation of the Dynamic Behavior of a Permanent Magnet Linear Actuator" (Simulación del comportamiento dinámico de un actuador lineal de imán permanente), Elec. Energ., vol. 23, núm. 1, pp. 37-43, 2010.
[5] I. Yatchev y E. Ritchie, "Simulation of Dynamics of a Permanent Manget Linear Actuator" (Simulación de la dinámica de un actuador lineal de imán permanente), International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, núm. 6, pp. 726-730, 2010.
[6] S.-M. Wang, T. Miyano y M. Hubbard, "Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator" (Análisis del campo electromagnético y simulación dinámica de un actuador de dos válvulas) IEEE Transactions on Magnetics, vol. 29, núm. 2, pp. 1741-1746, 1993.
[7] A. Radulian y N. Mocioi, "Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors" (Modelado numérico de un actuador electromagnético para contactores de vacío). Conferencia y Exposición Internacional sobre Ingeniería Eléctrica y de Potencia, Iasi, Rumania, 2014.
[8] N. Paudel, "Part 1: How to Model a Linear Electromagnetic Plunger" (Parte 1: Cómo modelar un émbolo electromagnético lineal), 7 de junio de 2016. [En Internet]. Disponible en: https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, "Part 2: Model a Linear Electromagnetic Plunger with a Blocker" (Parte 2: Modelo de un émbolo electromagnético lineal con un bloqueador), 14 de junio de 2016. [En Internet]. Disponible en: https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer y B. Ulrych, "Electromechanical Actuators Dynamics" (Dinámica de los actuadores electromecánicos), J. of Electrical Engineering, vol. 60, núm. 5, pp. 255, 2009.
[11] H. Musaab, "Using Lookup Tables to Model an Electromagnetic Suspansion System" (Uso de tablas de consulta para modelar un sistema de expansión electromagnética), American Journal of Applied Sciences, vol. 9, núm. 8, pp. 1199-1202, 2012.
[12] O. Vogel y J. Ulm, "Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics" (Teoría de solenoides proporcionales y cálculo de fuerzas magnéticas mediante el uso de Comsol Multiphysics), en Conferencia de Comsol, Stuttgart, 2011.
Análisis de actuadores electromagnéticos lineales utilizando FEA
RESUMEN
En este artículo, analizamos las características dinámicas de un actuador electromagnético, utilizado para cortacircuitos de vacío. Se analizan los fenómenos magnéticos, eléctricos y mecánicos de manera simultánea para obtener el comportamiento dinámico del actuador. Los parámetros magnéticos se computan utilizando el análisis de elementos finitos (FEA) y luego se importan al software de análisis dinámico, donde se calculan las ecuaciones eléctricas y mecánicas. Se presentan los resultados del análisis junto con algunos datos experimentales. Esta técnica se puede utilizar para analizar de una manera muy precisa el comportamiento electromagnético dinámico de sensores, relés, interruptores y otros sistemas de actuadores.
PLANTEAMIENTO DEL PROBLEMA
El actuador electromagnético es ampliamente utilizado en cortacircuitos. Su función es lograr el movimiento de los contactos móviles del frasco de vacío con determinadas velocidades y trayectorias precisas.
En este informe, se propone y analiza un nuevo modelo de un actuador lineal, que se utilizará en la próxima generación de los sistemas de línea de techo de material rodante de TE. Un factor que afecta en gran medida el funcionamiento del actuador es la fuerza de arrastre magnética. Esta fuerza podría deberse a los siguientes factores:
- Campo magnético estático: a medida que la estructura se mueve, experimenta una tracción magnética (debido al movimiento relativo con los imanes dependiendo de su posición).
- Corriente residual en la bobina: cuando el voltaje de retención se desconecta de la bobina, toma tiempo para que la corriente de la bobina disminuya a cero. Mientras está presente, produce una tracción magnética hacia la posición de cierre. La rápida disminución de la corriente se puede lograr mediante:
o Aumento del voltaje del supresor de voltaje transitorio (TVS)
o Disminución de la inductancia de la bobina
- Corrientes de Foucault inducidas [1]
- Corrientes de Foucault inducidas por el movimiento: este efecto representa la mayor parte de las pérdidas de energía (si hay un movimiento relativo entre la estructura y los imanes) y puede reducirse o incluso eliminarse efectivamente moviendo los imanes en la estructura (o usando imanes con menor intensidad de campo magnético) [1].
- Corriente de fuerza electromotriz (EMF) inversa: la estructura en movimiento causa voltaje de EMF inversa que a su vez causa corriente de EMF inversa que actúa contra el movimiento.
En investigaciones anteriores, no se había tenido en cuenta el efecto de las corrientes de Foucault en el movimiento de la estructura del actuador, pero, como elemento fundamental para el rendimiento del actuador, todos los efectos mencionados anteriormente se han tenido en cuenta, calculado e incluido en el modelo. Por lo tanto, nuestro modelo predice con alta precisión el comportamiento real del actuador antes de la creación de prototipos y se puede utilizar para el análisis de sensibilidad a fin de reducir el tiempo de diseño y el costo. De esta manera, se logra una solución técnica y económica óptima. En las siguientes secciones se brindará una descripción más detallada de los métodos y resultados.
MÉTODOS Y RESULTADOS
Análisis estático
En la figura 1 se muestra la estructura propuesta del actuador electromagnético:

En comparación con un actuador típico (que generalmente consta de una bobina de apertura y cierre), este tipo de actuador consta de la carcasa (o marco), el conector de acero, el conjunto de la bobina (bobina y carrete), la estructura (émbolo), el eje, la arandela de poliuretano y los imanes permanentes (PM) de samario-cobalto (SmCo).
Los devanados de la bobina crean un campo electromagnético cuando la corriente se aplica a través de sus terminales. El propósito de la bobina es accionar la estructura en la posición cerrada y ayudar a mantenerla allí. Este actuador debería fallar, a prueba de errores (abierto) en caso de pérdida de potencia en la bobina. El proceso de apertura comienza cuando se corta la corriente en la bobina y se logra solo por
medios mecánicos (resortes, etc.). Por lo tanto, la disipación de potencia (crítica para los trenes modernos) en este tipo de actuador es significativamente menor que la disipación en un actuador típico, mientras que la seguridad es una prioridad.
El estator concentra el campo magnético. Rodea el exterior de la bobina y está hecho de acero con bajo contenido de carbono según la clasificación 1018 del Instituto Estadounidense del Hierro y el Acero (AISI). El acero con bajo contenido de carbono se utiliza para la mayoría de los actuadores electromagnéticos. Tiene una alta permeabilidad y un costo relativamente bajo [12].
Los imanes producen una fuerza de retención, que depende de la posición de la estructura en relación con la carcasa (reluctancia magnética baja y alta).
Para el análisis, se ha seleccionado la física de los campos magnéticos. Para definir las propiedades magnéticas no lineales del acero al carbono y la densidad de flujo remanente de los imanes, se ha aplicado la Ley de Ampère a los dominios relevantes. Las propiedades magnéticas no lineales se introducen para dar cuenta de la saturación magnética (el estado en que la magnetización de un
material alcanza un punto en el que no puede aumentar más debido al aumento del campo magnético externo aplicado H) [2] [3].
Para el cálculo de la fuerza electromagnética en la estructura, se ha aplicado el método del tensor de tensión de Maxwell. Este tensor es matemáticamente una integral a lo largo de una trayectoria cerrada (en 2D) o un área de superficie cerrada "A" (en 3D) en torno a un dominio de interés. Una de las limitaciones de este método es que, cuando se aplica un material magnético a la interfaz de material magnético (que actúa como polos), se debe mantener un espacio de aire muy pequeño (<0,1 mm) entre ellos; de lo contrario, se calcula un valor muy bajo de la fuerza, que no corresponde a su valor real [12] [5].
Análisis dinámico
Para estudiar el comportamiento dinámico del actuador se han simulado dos modelos para dar cuenta de su rendimiento de apertura y cierre [4] [7] [8]. El circuito eléctrico utilizado para accionar el actuador se muestra a continuación (figura 2):

Durante la apertura, la corriente en la bobina se corta y se utiliza el TVS para suprimir el voltaje inducido (y en consecuencia la corriente inducida). Durante el cierre, se utiliza una secuencia de pulsos de la fuente de alimentación del actuador (APS) para accionar el actuador.
Las ecuaciones resueltas ((1) – (3)) son las siguientes:
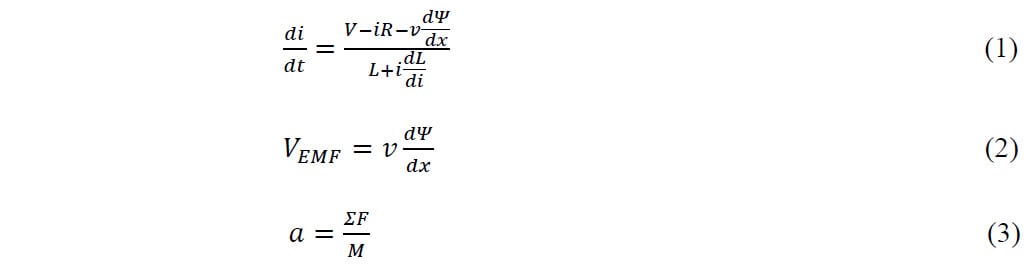
V: voltaje (V), i: corriente (A), R: resistencia (Ω), L: inductancia (H), VEMF: voltaje de EMF inversa (V), v: velocidad (m/s), α: aceleración (m/s2), t: tiempo (s) ΣF: fuerza total (N), M: masa (kg), Ψ: enlace de flujo (Wb-T). Los enlaces de flujo tienen dos componentes, uno de los cuales depende del campo magnético producido por el imán permanente sin escobillas (BPM) y otro componente debido al campo magnético producido por la bobina (Bc).
Las corrientes de Foucault se calcularon utilizando la siguiente ecuación [1]:
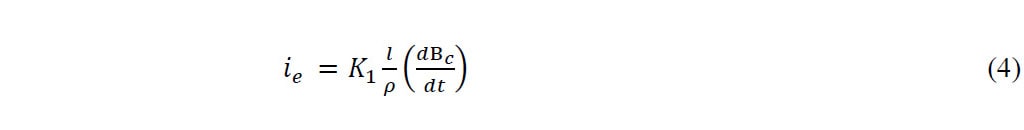
Donde K1 es un factor geométrico, l es la longitud del émbolo y ρ es la resistividad del material [1]. Suponiendo el émbolo como un cilindro, la ecuación 4 se convierte en lo siguiente:

El campo magnético producido por las corrientes de Foucault (Be) y la fuerza correspondiente (Fe) se calcularon utilizando las ecuaciones 6 y 7.
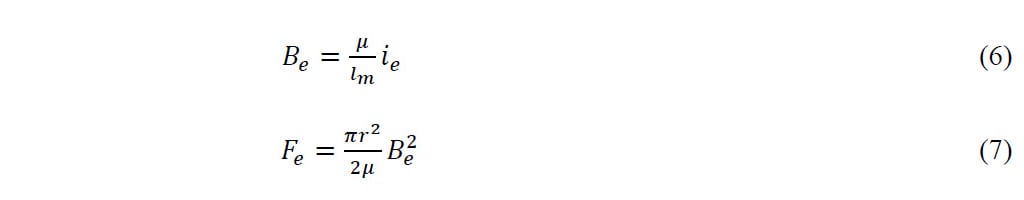
Donde lm es la trayectoria magnética, r es el radio del émbolo y μ la permitividad del material.
Resultados de la simulación
La distribución del campo magnético en diferentes posiciones se muestra en la figura 3.
En la posición cerrada (figura 3a), la estructura junto con la carcasa de acero forma una trayectoria de baja reluctancia magnética, mientras que el gran espacio en la parte superior representa una trayectoria de alta resistencia magnética. Por lo tanto, las líneas del campo magnético atraviesan casi exclusivamente el extremo de la estructura que está en contacto con la carcasa. La fuerza de retención producida por los imanes en esta
posición es de alto valor. Para lograr una operación a prueba de fallas, también se utiliza la bobina para producir una fuerza de retención aún mayor y mantener la estructura en la posición cerrada.
Para la apertura, la corriente que fluye a través de la bobina se corta y la estructura comienza a moverse. A medida que la estructura se mueve desde la posición cerrada a la abierta, las líneas del campo magnético se empujan hacia la trayectoria previamente inferior (figura 3b), ya que ahora el espacio de aire en la posición abierta es cada vez más pequeño (la reluctancia magnética es cada vez menor). Por lo tanto, la fuerza de retención en la parte inferior disminuye, mientras que la atracción en la parte superior aumenta.

Cuando la estructura alcanza la posición abierta (figura 3c), la trayectoria de reluctancia es opuesta a la mencionada anteriormente, por lo que las líneas del campo magnético se concentran principalmente en la parte superior. Como se muestra, la concentración del campo magnético no es similar cuando la estructura está en posición cerrada y abierta. Por lo tanto, la fuerza de retención en la posición abierta tendrá un valor más bajo que la que está en la posición cerrada. Los resultados del análisis dinámico se muestran en las figuras 4 y 5:


Algunos resultados experimentales preliminares (figuras 6 y 7) en modelos de actuadores ligeramente diferentes (diseños anteriores a los ajustes finales) demuestran el concepto del diseño propuesto y el circuito de control.

El perfil de las características dinámicas observadas durante las pruebas se condice con los resultados de la simulación. Los valores de la velocidad y la duración de la operación de cierre y apertura son similares en pruebas y simulaciones (menos del 10 % de error).
ANÁLISIS Y PUNTOS CLAVE
Se propone el modelo optimizado del actuador para minimizar o incluso eliminar el efecto del frenado electromagnético debido a la inducción. Se utiliza un nuevo circuito de control para suprimir este efecto durante la apertura, mientras que, durante el cierre, se introduce una secuencia pulsante para controlar el rendimiento del actuador.
El innovador diseño del actuador y el circuito de control que mejora la eficiencia y el rendimiento del sistema (baja disipación de potencia) contribuyen significativamente al desarrollo continuo de la próxima generación de sistemas de línea de techo para trenes de TE. El diseño del actuador permite lograr un funcionamiento fiable y se ajusta a los requisitos de perfil bajo y de ligereza del mercado
(mejora del rendimiento aerodinámico) y consume un nivel mínimo de energía.
Sobre la base de la comparación entre los resultados de las pruebas y la simulación, se llega a la conclusión de que el método de cálculo propuesto permite analizar con precisión las características transitorias de un actuador electromagnético. Sin embargo, cabe mencionar que, en este informe, se tiene en cuenta la contribución de la corriente de Foucault, lo que no sucede en la mayoría de los documentos existentes debido a su
forma complicada. Por lo tanto, la importancia de este método es que se puede utilizar antes de la creación de prototipos para reducir significativamente el tiempo, el costo y los recursos durante el diseño y la fabricación.
AGRADECIMIENTOS
Queremos agradecer a Graham Mcdonald, Robert Phillpotts y Thomas Moore por todo el apoyo y el asesoramiento experto que brindaron a lo largo de este proyecto. Proporcionaron los modelos mecánicos y las configuraciones electrónicas siguiendo las recomendaciones del análisis y los datos para las fuerzas mecánicas.
REFERENCIAS
[1] Mandache, L.; D. Topan; K. Al Haddad. “Modeling of Non-Linear Ferromagnetic Cores” (Modelado de núcleos ferromagnéticos no lineales). Revue Roumaine de Sciences Techniques. Serie Electrotechnique et Energetique. Vol. 53, número 4. 2008.
[2] K. Srairi y M. Feliachi, "Numerical Coupling Moldels for Analyzing Dynamic Behaviors of Electromagnretic actuators" (Modelos de acoplamiento numérico para analizar el comportamiento dinámico de los actuadores electromagnéticos), IEEE Transactions on Magnetics, vol. 34, núm. 5, pp. 3608-3611, 1998.
[3] I. Yatchev, V. Gueorgiev, K. Hinov, R. Ivanov y D. Dimitrov, "Dynamic characteristics of a permanent magnet electromagnetic valve actuator" (Características dinámicas de un actuador de válvula electromagnética de imán permanente), en la 12.ª Conferencia Internacional sobre Optimización de Equipos Eléctricos y Electrónicos, 2010.
[4] I. Yatchev, V. Gueorgiev, R. Ivanov y K. Hinov, "Simulation of the Dynamic Behavior of a Permanent Magnet Linear Actuator" (Simulación del comportamiento dinámico de un actuador lineal de imán permanente), Elec. Energ., vol. 23, núm. 1, pp. 37-43, 2010.
[5] I. Yatchev y E. Ritchie, "Simulation of Dynamics of a Permanent Manget Linear Actuator" (Simulación de la dinámica de un actuador lineal de imán permanente), International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, vol. 4, núm. 6, pp. 726-730, 2010.
[6] S.-M. Wang, T. Miyano y M. Hubbard, "Electromagnetic Field Analysis and Dynamic Simulation of a Two-Valve Actuator" (Análisis del campo electromagnético y simulación dinámica de un actuador de dos válvulas) IEEE Transactions on Magnetics, vol. 29, núm. 2, pp. 1741-1746, 1993.
[7] A. Radulian y N. Mocioi, "Numerical Modelling of an Electromagnetic Actuator for Vacuum Contactors" (Modelado numérico de un actuador electromagnético para contactores de vacío). Conferencia y Exposición Internacional sobre Ingeniería Eléctrica y de Potencia, Iasi, Rumania, 2014.
[8] N. Paudel, "Part 1: How to Model a Linear Electromagnetic Plunger" (Parte 1: Cómo modelar un émbolo electromagnético lineal), 7 de junio de 2016. [En Internet]. Disponible en: https://www.comsol.co.in/blogs/part-1-how-to-model-a-linear-electromagnetic-plunger/.
[9] N. Paudel, "Part 2: Model a Linear Electromagnetic Plunger with a Blocker" (Parte 2: Modelo de un émbolo electromagnético lineal con un bloqueador), 14 de junio de 2016. [En Internet]. Disponible en: https://www.comsol.co.in/blogs/part-2-model-a-linear-electromagnetic-plunger-with-a-blocker/.
[10] D. Mayer y B. Ulrych, "Electromechanical Actuators Dynamics" (Dinámica de los actuadores electromecánicos), J. of Electrical Engineering, vol. 60, núm. 5, pp. 255, 2009.
[11] H. Musaab, "Using Lookup Tables to Model an Electromagnetic Suspansion System" (Uso de tablas de consulta para modelar un sistema de expansión electromagnética), American Journal of Applied Sciences, vol. 9, núm. 8, pp. 1199-1202, 2012.
[12] O. Vogel y J. Ulm, "Theory of Proportional Solenoids and Magnetic Force Calculation using Comsol Multiphysics" (Teoría de solenoides proporcionales y cálculo de fuerzas magnéticas mediante el uso de Comsol Multiphysics), en Conferencia de Comsol, Stuttgart, 2011.
